但凡教材不是英文的
前言
第一门需要做笔记的课程。
内容高中数学和OI都搞过,主要问题是英文授课,得能看懂题目。
下面全是从『离散数学及其应用(第八版)』和中文版『离散数学及其应用(第六版)』抠出来的。
重拾$\LaTeX$。
英汉大词典(雾)
1 命题逻辑和证明
1.1 命题逻辑
- proposition:命题
- propositional variables/sentential variables:代指命题的字母(命题变量)
- truth value:命题的真假
- atomic propositions:最简命题
- compound propositions:复合命题
- logical operators:逻辑运算符
- connectives:二元以上的逻辑运算符
- truth table:真值表
- negation operator:非
- conjunction:与(合取)
- disjunction:或(析取)
- exclusive or:异或
- conditional statement/implication:$p\rightarrow q$
- hypothesis/antecedent/premise:$p$
- conclusion/consequence:$q$
- 当且仅当$p$真$q$假时$p\rightarrow q$为假
- 人话:“if p, then q” “p implies q”
“if p, q” “p only if q”
“p is sufficient for q” “a sufficient condition for q is p”
“q if p” “q whenever p”
“q when p” “q is necessary for p”
“a necessary condition for p is q” “q follows from p”
“q unless ¬p” “q provided that p” - converse:$q\rightarrow p$(逆命题)
- contrapositive:$\lnot q\rightarrow \lnot p$(倒置命题,与原命题等价)
- inverse:$\lnot p\rightarrow \lnot q$(反命题)
- equivalent:等价
- biconditional statement/bi-implications:$p\leftrightarrow q$
- 人话:“p if and only if q”“p is necessary and sufficient for q”
“if p then q, and conversely”
“p iff q.” “p exactly when q.”
- 人话:“p if and only if q”“p is necessary and sufficient for q”
- Boolean variable:布尔变量
- bit operations:位运算
- bitwise:按位
1.2 命题逻辑的应用
- represent
- System Specifications:系统规范
- logic circuit/digital circuit:逻辑门
- inverter:非门
1.3 命题等价
- tautology:永真式
- contradiction:永假式
- contingency:不永式
- $p\equiv q$:$p\leftrightarrow q$永真(逻辑等价)
- $p\rightarrow q\equiv \lnot p\lor q$(conditional-disjunction equivalence)
- De Morgan’s Laws:$\lnot(p\land q)\equiv\lnot p\lor\lnot q\\\lnot(p\lor q)\equiv\lnot p\land\lnot q$
- satisfiable:不永假
- solution:让命题$T$的一组解
- disjunctive normal form:$(p_1\land p_2 \land p_3)\lor(\lnot p_1\land p_2\land p_3)\lor(\lnot p_1\land\lnot p_2\land p_3)$(析取范式)
- 列真值表,找$T$的行,行内合取,不同行析取
- conjunctive normal form:$(p_1\lor p_2 \lor p_3)\land(\lnot p_1\lor p_2\lor p_3)\land(\lnot p_1\lor\lnot p_2\lor p_3)$(合取范式)
- 列真值表,找$F$的行,行内取反析取,不同行合取
1.4 谓词和量词
- predicate:谓词
- quantifiers:量词
- propositional function:命题函数
- n-place predicate/n-ary predicate:n元命题函数
- preconditions:输入满足的条件(前置条件)
- postconditions:输出满足的条件(后置条件)
- quantification:从命题函数产生命题(量化)
- predicate calculus:处理谓词和量词的逻辑领域(谓词演算)
- universal quantification:$\forall xP(x)$(全称量化)
- domain of discourse/universe of discourse:论述范围
- counterexample:反例
- universal quantifier:$\forall$(全称量词)
- 人话:“for all”“for every”“all of,” “for each,” “given any,” “for arbitrary,” “for each,” and “for any”
- existsential quantification:$\exists xP(x)$(存在量化)
- existsential quantifier:$\exists$(存在量词)
- 人话:“There is an x such that P(x),”
“There is at least one x such that P(x),”“For some xP(x).”
- uniqueness quantifier:$\exists !$(唯一量词)
1.5 嵌套量词
- nested quantifier:$\forall x\exists y\forall z$(嵌套量词)
1.6 推理规则
- argument:论证
- valid:有效性
- premises:前提
- argument form:论证中,命题变量代替命题(论证形式)
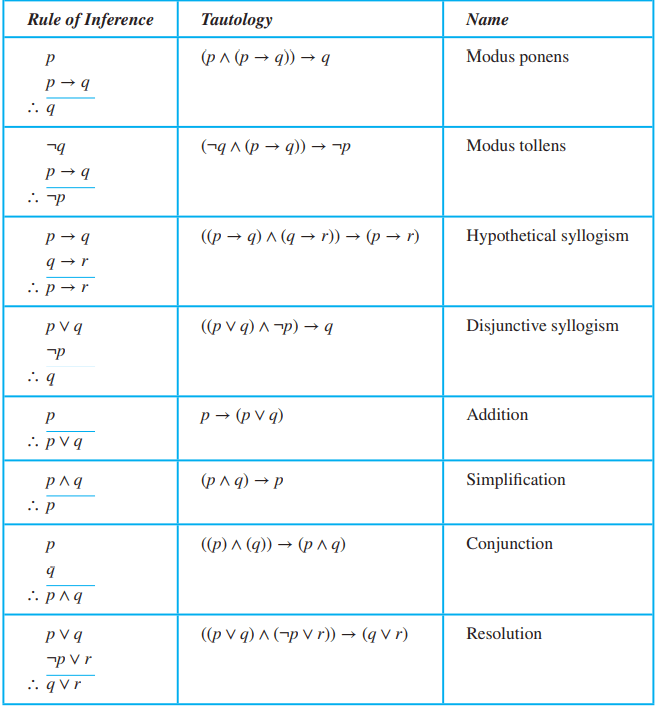
- fallacies:谬误(不正确推理)
- fallacy of affirming the
conclusion:$\because p\rightarrow q,q\therefore p$(肯定结论谬误) - fallacy of denying the hypothesis:$\because p\rightarrow q,\lnot p\therefore \lnot q$(否定假设谬误)
- fallacy of affirming the
- Universal instantiation:$\because\forall xP(x)\therefore P(c)$(全称例示)
- Universal generalization:$\because P(c)\ for\ an\ arbitrary\ c\therefore\forall xP(x)$(全称生成)
- existsential instantiation:$\because\exists xP(x)\therefore P(c)\ for\ some\ element\ c$(存在例示)
- existsential generalization:$\because P(c)\ for\ some\ element\ c\therefore \exists xP(x)$(存在生成)
- universal modus ponens:$\because\forall x(P(x) \rightarrow Q(x)),P(a)\ where\ a\ is\ a\ particular\ element\ in\ the\ domain\therefore Q(a)$(全称假言推理)
- universal modus tollens:$\because\forall x(P(x)\rightarrow Q(x)),\lnot Q(a)\ where\ a\ is\ a\ particular\ element\ in\ the\ domai\therefore\lnot P(a)
$(全称取拒式)
1.7 证明导论
- theorem:定理
- lemma:引理
- corollary:推论
- conjecture:猜想
- direct proof:直接证明
- same/opposite parity:奇偶相同/不同
- perfect square:完全平方数
- proof by contraposition:要证$p\rightarrow q$,即证$\lnot q\rightarrow \lnot p$(反证法)
- trivial proof:用$q$为真证明$p\rightarrow q$为真
- proofs by contradiction:要证$p$,即证$\lnot p\rightarrow(r\land\lnot r)$
- begging the question/circular reasoning:证明中用到了未知正确性的待证论题(偷用论题/循环论证)
1.8 证明的方法和策略
- $\left(\bigvee\limits_{i=1}^np_i\right)\rightarrow q\leftrightarrow\bigwedge\limits_{i=1}^n(p_i\rightarrow q)$
- exhaustive proof/proofs by exhaustion:测试所有情况以证明(穷举证明)
- perfect power:$n^\alpha(n,\alpha\in Z,a\gt1)$(全幂数)
- proof by cases:找出所有情况,分别证明(分情形证明)
- without loss of generality:证明一种情形,可以简单地推到另一种情形(不失一般性),简写为WLOG
- existence proof:证明$\exists xP(x)$(存在性证明)
- constructive:找出$c$满足$P(c)$的证明(构造性的)
- witness:找到的$c$
- nonconstructive:不找$c$的证明(非构造性的)
- constructive:找出$c$满足$P(c)$的证明(构造性的)
- uniqueness proof:证明$\exists!xP(x)$(唯一性证明),有如下两步
- existence:证明$P(x)$
- uniqueness:证明如果$P(y)$,则$y=x$
- forward and backward reasoning:前推和后推
- rational number:有理数
- arithmetic mean:$\dfrac{\sum\limits_{i=1}^na_i}{n}$(算术平均数)
- geometric mean:$\sqrt[n]{\prod\limits_{i=1}^na_i}$(几何平均数)
- harmonic mean:$\dfrac{n}{\sum\limits_{i=1}^n\frac{1}{a_i}}$(调和平均数)
- quadratic mean:$\sqrt{\dfrac{\sum\limits_{i=1}^na_i^2}{n}}$(平方平均数)
- tile:填充
- checkerboard:若干方格组成的矩形棋盘
- standard checkerboard:$8\times8$的棋盘
- domino:$1\times2$的骨牌
- Fermat’s last theorem:若$xyz\neq0$,则$x^n+y^n=z^n(n\ge2)$无整数解(费马大定理)
2 集合与函数
2.1 集合
- set:集合
- contain:包含
- elements/members:集合的成员
- roster method:$\{a,b,c,d\}$(穷举表示集合)
- set builder:$\{x|\dots\}$(构造符号表示)
- empty set/null set:空集
- singleton set:只有一个元素的集合
- universal set:全集
- Venn diagram:维恩图
- subset:子集
- superset:超集
- proper subset:真子集
- finite set:有限集
- cardinality:集合元素的个数,记作$|S|$(基数)
- power set:所有子集的集合,记作$\Rho(S)$(幂集合)
- ordered n-tuple:$(a_1,a_2,\dots,a_n)$(有序$n$元组)
- ordered pairs:有序二元组
- Cartesian product:$A\times B=\{(a,b)|a\in A\land b\in B\};A_1\times A_2\times\dots\times A_n=\{(a_1,a_2,\dots,a_n)|a_i\in A_i\ for\ i=1,2,\dots,n\}$(笛卡尔积)
- $A\times B$的一个子集称为$a\ relation\ from\ the\ set\ A\ to\ the\ set\ B$
- $A\times A$的一个子集被称为$a\ relation\ on\ A$
- truth set:$\{x\in D|P(x)\}$(真值集合)
2.2 集合操作
- union:$A\cup B$(并集)
- intersection:$A\cap B$(交集)
- disjoint:$A\cap B=\emptyset$
- principle of inclusion–exclusion:$|A\cup B|=|A|+|B|-|A\cap B|$(容斥原理)
- complement
of B with respect to A/difference:$A-B$(差集) - complement:$\overline{A}$(补集)
- membership tables:成员表,类似真值表
- multiset:$\{m_1\cdot a_1,m_2\cdot a_2,\dots,m_n\cdot a_n\}$(可重集)
- multiplicities:元素出现的次数$m_i$
- 并集$m_i$取$\max$,交集$m_i$取$\min$,差集$m_i$相减(最小为$0$),和集(sum)$m_i$相加
2.3 函数
设函数$f$定义域为$A$,值域为$B$
- domain:定义域
- codomain:值域
- image/preimage:$a/b(f(a)=b)$
- injective/one-to-one:$f(a)=f(b)\iff a=b$(单射)
- (strictly)increasing/decreasing:(严格)单增/单减
- surjective/onto:$\forall b\in B,\exists a\in A,f(a)=b$(满射)
- one-to-one correspondence/bijection:双射(单射+满射)
- inverse function:反函数$f^{-1}$
- $(f\circ g)(x):f(g(x))$
- graph:$\{(a,b)|a\in A,b=f(a)\}$(图像)
- floor function/ceiling function:向下取整/向上取整函数
- factorial function:阶乘函数
- partial function/total funtion:定义域残缺/完整
2.4 数列与求和
- sequence:数列
- term:数列的项
- geometric progression:几何数列(等比数列)
- initial term:首项
- common ratio:公比
- arithmetic progression:等差数列
- initial term
- common difference:公差
recurrence relation:递推关系
- solution of a recurrence relation:有递推关系的数列
- initial conditions:递推的初始条件
- Fibonacci sequence:$f_0=0,f_1=1$
iteration:递推公式推通项的一种方法,有下面两种(e.g. $a_n=a_{n-1}+3,a_1=2$):
forward substitution:
$a_2=2+3\\a_3=(2+3)+3=2+2\cdot 3\\a_4=(2+2\cdot 3)+3=2+3\cdot 3\\\dots\\a_n=a_{n−1}+3=(2+3\cdot(n−2))+3=2+3(n−1)$
backward substitution:
$a_n=a_{n−1}+3\\=(a_{n−2}+3)+3\\=a_{n−2}+3\cdot2\\=(a_{n−3}+3)+3\cdot2\\=a_{n−3}+3\cdot3\\\dots\\=a_2+3(n−2)\\=(a_1+3)+3(n−2)\\=2+3(n−1)$
- summation:求和(e.g.$\sum\limits_{i=m}^na_i$)
- index of summation:$i$(求和下标)
- lower limit/upper limit:$m$/$n$
2.5 基数
- countable:集合是有限集或其基数与自然数集相同(可数)
- uncountable:不uncountable
- aleph null:可数的无限集合用$|S|=\aleph_0$表示其个数
- $countable\cup countable = countable$
- computable:计算机已经算出来的函数
- uncomputable:不computable
3 算法
3.1 算法
- pseudocode:伪代码
- searching problems:在有序的列表中找特定元素
- linear search/sequential search:暴力循环
- binary search:二分
- sort
- bubble sort:冒泡排序
- insertion sort:插排
- string matching:字符串匹配
- pattern:模式串
- text:母串
- shift:匹配的首地址
- naive string matcher:暴力$O(nm)$循环
- greedy algorithms:贪心
- optimization problems:找最优解的问题
- cashier’s algorithm:用最少的硬币找零
- halting problem:能否设计一个函数,传入任意源代码和其输入,判断程序能否在有限时间算出(无解)
- mode:众数
3.2 函数的走势
- big-O notation:如果$\exists C,k,|f(x)|\le C|g(x)|$对$\forall x>k$成立,则称$f(x)\ is\ O(g(x))$
- witnesses to the relationship f(x) is O(g(x)):$C,k$
- $f_1\ is\ O(g_1),f_2\ is\ (g_2)$,则$f_1+f_2\ is\ O(\max\{g_1,g_2\}),f_1f_2\ is\ O(g_1g_2)$
- big-Omega notation:如果$\exists C>0,k,|f(x)|\ge C|g(x)|$对$\forall x>k$成立,则称$f(x)\ is\ \Omega(g(x))$
- big-Theta notation:若$f(x)\ is\ O(g(x)),f(x)\ is\ \Omega(g(x))$,则称:
- $f(x)\ is\ \Theta(g(x))$
- $f(x)\ is\ big-Theta\ of\ g(x)$
- $f(x)\ is\ of\ order\ g(x)$
- $f(x)\ and\ g(x)\ are\ of\ the\ same\ order$
- $f(x)\ is\ \Omega(g(x))\leftrightarrow g(x)\ is\ \Omega(f(x))$
3.3 函数复杂度
- computational complexity:计算复杂度
- time complexity:时间复杂度
- space complexity:空间复杂度
- worst-case complexity:最坏情况
- average-case complexity:平均
- brute-force algorithm:暴力算法

- tractable:最坏$\Theta(n^b)$
- intractable:不tractable
- class NP:可以$\Theta(n^b)$验证答案的问题
- class P:tractable的问题
- NP-complete problems:如果其中任何问题可用多项式复杂度解决,则所有$NP$都能用多项式复杂度解决(NP完全问题)
- P versus NP:$P$是否等于$NP$
4 同余
4.1 除和模
- 如果$a|b$:
- a divides b
- a is a factor or divisor of b
- b is a multiple of a
- dividend:被除数
- divisor:除数
- quotient:商
- remainder:余数
- a is congruent to b modulo m:$a\equiv b\pmod m$
- 亦称a and b are congruent modulo m
- congruence:同余式
- modulus(pl. moduli):m
- $a+_mb=(a+b)\mod m$
- $a\cdot _mb=(a\cdot b)\mod m$
4.2 整数的表示
- base b expansion of n:$n=\sum\limits_{k=0}^{\infty}a_kb^k$
- decimal expansions:十进制展开
- binary expansions:二进制展开
- octal expansions:八进制展开
- hexadecimal expansions:十六进制展开
- Fast Modular Exponentiation:快速幂
4.3 质数&最大公约数
- prime:质数
- composite:合数
- trial division:用$\le\sqrt{n}$的质数判断$n$是否为质数
- sieve of Eratosthenes:埃氏筛
- $\pi(x)$:$\le x$的质数个数,接近于$\dfrac{x}{\ln x}$
- greatest common divisor of a and b:$\gcd(a,b)$
- a and b are relatively prime:$a\perp b$(互质)
- pairwise relatively prime:一堆数两两互质
- least common multiple:$lcm$
- The Euclidean Algorithm:辗转相除法
- $\exists s,t\in\mathbb{Z},\gcd(a,b)=sa+tb$
- Bezout coefficients of a and b:s,t
- Bezout’s identity:等式$\gcd(a,b)=sa+tb$
4.4 逆元
- inverse:逆元
- The Chinese Remainder Theorem:中国剩余定理
$\boxed{\begin{matrix}x\equiv a_1\pmod {m_1}\\x\equiv a_2\pmod {m_2}\\\vdots\\x\equiv a_n\pmod {m_n}\end{matrix}}$
$\boxed{\begin{matrix}m=\prod\limits_{i=1}^nm_i\\M_k=\dfrac{m}{m_k}\\y_k\equiv M_k^{-1}\pmod {m_k}\\x\equiv\sum\limits_{i=1}^na_iM_iy_i\pmod m\end{matrix}}$
- Fermat’s Little Theorem:费马小定理
- $a^{p-1}\equiv1\pmod p(p\in \mathbb{P},p\nmid a)$
- $a^p\equiv a\pmod p(p\in\mathbb{P})$
- pseudoprimes to the base b:满足$b^{n-1}\equiv1\pmod n$的合数$n$(伪素数)
- Carmichael number:满足对$\forall b\perp n$有$b^{n-1}\equiv1\pmod n$的合数$n$
- primitive root:原根
- 若$g^k\mod m(0\le g,k\le m-1)$两两不同,则$g$为模数$m$的原根
- 若$g^b\equiv a\pmod m$,则称b is the discrete logarithm of a modulo m to the base g
4.5 同余的应用
- Hashing Functions:哈希
- Pseudorandom Numbers:伪随机数
- linear congruential method:$x_{n+1}=(ax_n+c)\mod m$
- modulus:m
- multiplier:a
- increment:c
- seed:$x_0$
- pure multiplicative generator:$c=0$
5 归纳&递归
5.1 数学归纳法
- mathematical induction:数学归纳法
- 设$P(n)$
- $Basis\ Step:P(1)\ is\ true$
- $Inductive\ Step:\forall k,P(k)\rightarrow P(k+1)\ is\ true$
- harmonic series:调和级数
5.2 强数学归纳&井井有序
- strong induction:强数学归纳
- $\forall k,P(1)\land P(2)\land\dots P(k)\rightarrow P(k+1)\ is\ true$
5.3 递归定义&结构化归纳
- recursion/inductive definition:递归定义的函数
- basis step:初始定义
- recursive step:递归规则
- exclusion rule:例外规则
6 数数
6.1 数数基础
- product rule:乘法原理
- sum rule:加法原理
- the subtraction rule/principle of inclusion–exclusion:容斥原理
- tree diagrams:树状图
6.2 抽屉原理
- The Pigeonhole Principle:抽屉原理
- n个物品放到n+1个盒子里,则至少有一个盒子有不少于1个物品
- k+1个元素的集合到k个元素的集合的函数一定不单射
- n个物品放到k个盒子里,至少有一个盒子有不少于$\left\lceil\dfrac{n}{k}\right\rceil$个物品
- 任何长为$n^2+1$的实数列一定存在一个长为$n$的严格单增或单减的子数列
6.3 排列组合
- permutation:$P(n,r)$(排列)
- r-permutation:r个数的排列
- combination:$C(n,r)\dbinom{n}{r}$(组合)
- binomial coefficient:二项式系数
- combinatorial proof:组合数证明
6.4 二项式系数和一堆等式
- The Binomial Theorem:二项式定理
- pascal’s identity:$C_{n+1}^m=C_n^m+C_n^{m-1}$
- Pascal’s triangle:杨辉三角
- vandermonde’s identity:范德蒙德恒等式
- $C_{n+1}^{r+1}=\sum\limits_{i=r}^nC_i^r$
6.5 广义的排列组合?
- with repetition:可重
- $x_1+x_2+\dots+x_n=r(x_i\ge0)$:$C_{n+r-1}^{n-1}$
- $x_1+x_2+\dots+x_n=r(x_i>0)$:$C_{r-1}^{n-1}$
- Stirling numbers of the second kind:第二类斯特林数
8 进阶数数技巧
8.2 线性递推关系
- linear homogeneous recurrence:$a_n=c_1a_{n-1}+c_2a_{n-2}+\ldots+c_ka_{n-k}$(线性齐次递推关系)
- root:方程的解
- multiplicity:方程某个根的重数
- 对递推关系$a_n=c_1a_{n-1}+c_2a_{n-2}+\ldots+c_ka_{n-k}$,解特征方程$r^k-c_1r^{k-1}-\ldots-c_k=0$得根$r_1,r_2\ldots r_t$和对应重数$m_1,m_2\ldots m_t$,则$a_n=\sum\limits_{i=1}^nr_i^n\sum\limits_{j=0}^{m_i-1}\alpha_{i,j}n^j$,$\alpha_{i,j}$的值由初始条件确定
- linear nonhomogeneous recurrence relation with constant coefficients:$a_n=c_1a_{n-1}+c_2a_{n-2}+\ldots+c_ka_{n-k}+F(n),F(n)\neq0$且$F(n)$只与$n$有关(常系数线性非齐次递推关系)
- associated homogeneous recurrence relation:上面那个去掉$F(n)$的递推关系(关联齐次递归关系)
- 对常系数线性非齐次递推关系,若$\{a_n^{(p)}\}$为其一个特解(即忽略初始条件的解),$\{a_n^{(h)}\}$为其关联齐次递推关系的解,则其解为$a_n=a_n^{(p)}+a_n^{(h)}$
- 若$F(n)=s^n\sum\limits_{i=0}^tb_in^i$,$s$为关联齐次递归关系的特征方程根且重数为$m$,则有特解$a_n^{(p)}=n^m\sum\limits_{i=0}^tp_in^i$;否则有特解$a_n^{(p)}=\sum\limits_{i=0}^tp_in^i$(即$m=0$)
- 若$F(n)=G(n)+H(n)$,$a_n=\sum\limits_{i=1}^kc_ia_{n-i}+F(n),p_n=\sum\limits_{i=1}^kc_ip_{n-i}+G(n),q_n=\sum\limits_{i=1}^kc_iq_{n-i}+H(n)$,则$a^{(p)}_n=p^{(p)}_n+q^{(p)}_n$
8.4 生成函数
- generating function for the sequence :数列的生成函数$\sum\limits_{n=0}^\infty a_nx^n$
- ordinary generating function:普通型生成函数
- extended binomial coefficient:广义二项式系数$C_n^k=\begin{cases}\dfrac{n(n-1)\ldots(n-k+1)}{k!}&k>0\\0&k=0\end{cases}$
- the extended binomial theorem:广义二项式定理
8.5 容斥
- the principle of inclusion-exclusion:容斥原理$|A_1\cup A_2\cup\ldots\cup A_n|=\sum\limits_{1\le i\le n}|A_i|-\sum\limits_{1\le i<j\le n}|A_i\cap A_j|+\sum\limits_{1\le i<j<k\le n}|A_i\cap A_j\cap A_k|-\ldots+(-1)^{n+1}|A_1\cap A_2\cap\ldots\cap A_n|$
- derangement:错排
9 关系
9.1 关系和其性质
- binary relation from A to B:$A\times B$的一个子集
- A relation on a set A:$A\times A$的一个子集
- reflexive:$\forall a\in A,(a,a)\in R$
- symmetric:$\forall a,b\in A,(a,b)\in R\leftrightarrow (b,a)\in R$
- antisymmetric:$\forall a,b\in A,(a,b)\in R\land(b,a)\in R\rightarrow a=b$
- transitive:$\forall a,b,c\in A,(a,b)\in R\land(b,c)\in R\rightarrow (a,c)\in R$
- composite:若关系$R:A\rightarrow B,S:B\rightarrow C$,则$\forall b\in B,(a,b)\in R\land(b,c)\in S\rightarrow (a,c)\in S\circ R$
- $R^{n+1}=R^n\circ R$
- $R\ is\ transitive\leftrightarrow\forall n,R^n\subseteq R$
9.3 表示关系
- Matrix:矩阵表示$A=\{a_i\},B=\{b_i\},m_{ij}=\begin{cases}1&(a_i,a_j)\in R\\0&(a_i,a_j)\notin R\end{cases}$
- digraph/directed graph:用有向图表示
- vertex(pl. vertices)/node:节点
- edge/arc:边
- initial vertex:边的起点
- terminal vertex/end vertex:终点
- loop:自环
9.4 传递闭包
- transitive closure:传递闭包$R^\ast$
- path:图的路径
- circuit/cycle:起点和终点相同的路径(环)
- $R^\ast=\bigcup\limits_{i=1}^nR^i$
- Warshall algorithm:$W_k=[w_{ij}^{[k]}]$表示只允许走编号不超过$k$的节点作为中间节点的路径(不包括起终点),$i,j$的连通性矩阵,则$M_{R^\ast}=W_n,w_{ij}^{[k]}=w_{ij}^{[k-1]}\lor(w_{ik}^{[k-1]}\land w_{kj}^{[k-1]})$
9.5 等价关系
- equivalence relation:reflexive, symmetric, and transitive(等价关系)
- equivalent:两个元素能被等价关系关联,记为$a\thicksim b$
- equivalence class:在等价关系$R$中与$a$关联的所有元素的集合,记为$[a]_R$(只考虑$R$时可省略$R$)
9.6 偏序关系
- partial ordering or partial order:reflexive, antisymmetric, and transitive(偏序关系)
- partially ordered set/poset:集合$S$和一个偏序关系$R$,记作$(S,R)$
- comparable:要么$(a,b)\in R$,要么$(b,a)\in R$
- incomparable:$(a,b)\notin R,(b,a)\notin R$
- totally ordered/linearly ordered set/chain:$(S,R)$中所有元素对都$comparable$,$R$被称为total order/linear order(全序集)
- upper bound:$(S,R)$中,$A$为$S$的一个子集$\forall a\in A,a\preccurlyeq u$的$u$
- lower bound:上面的反义
- least upper bound:所有的upper bound中最小的
- greatest lower bound:上面的反义
- maximal:没有$a\prec b$
- minimal:没有$b\prec a$
- greatest element:$\forall b,b\preccurlyeq a$
- least element:$\forall b,a\preccurlyeq b$
- dual:$(S,R^{-1})$,其中如果$(a,b)\in R$,则$(b,a)\in R^{-1}$
- Hasse diagram:哈斯图
- y covers x:y覆盖x,$x\prec y$且不存在$z$使得$x\prec z\prec y$
- 构造哈斯图:如果y覆盖x,则把y画在x上面并用无向线段连接x,y
10 图论
10.1 图
- endpoints:边两边的端点,边connect its endpoints
- infinite graph:边集或点集无限
- simple graph:无重边无自环的无向图(简单图)
- simple directed graph:简单有向图
- multigraphs:允许有重边无自环的无向图
- pseudograph:重边自环都允许的无向图
- mixed graph:既有无向边又有有向边
10.2 图的术语和常见的图
- adjacent/neighbors:无向图中两点相邻,连接它们的边被称为incident with the vertices u
and v - neighborhood:与$v$相邻的点集$N(v)$
- degree:度数$\deg(v)$,自环算2度
- isolated:度数为0
- pendant:度数为1
- $\sum\limits\deg(i)=2m$
- 无向图中,奇度数的点有偶数个
- 有向图中有边(u,v),则称u is adjacent to v或v is adjacent from u
- in-degree:入度$\deg^-(v)$
- out-degree:出度$\deg^+(v)$
- $\sum\limits\deg^-(v)=\sum\limits\deg^+(v)=m$
- complete graph:完全图,记作$K_n$
- cycle:环,$V=\{(v_1,v_2),(v_2,v_3)\ldots,(v_n,v_1)\}$,记作$C_n$
- wheel:记作$W_n$
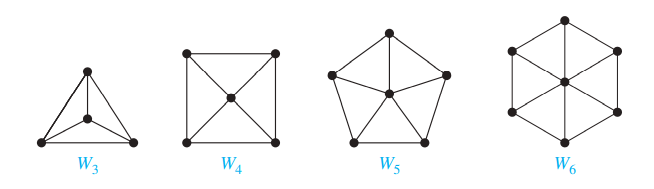
- n-dimensional hypercube/n-cube:记作$Q_n$
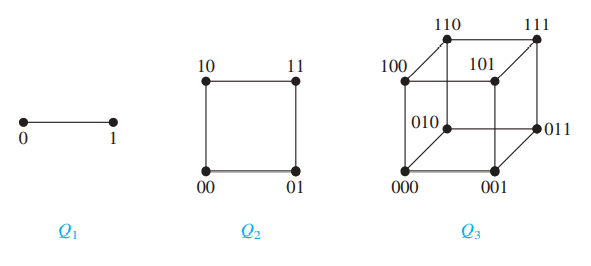
- bipartite graphs:二分图
- 一个简单图是二分图等价于能给每个点黑白染色且相邻点异色
- $K_{m,n}$:两边分别有$m,n$个节点的完全二分图
- subgraph:子图
- subgraph induced by a subset W:点集为W,边集为所有连接W中的点的边
- union:两个图组合,记作$\cup$
10.3 图的表示
- adjacency lists:邻接表
- 无向图

- 有向图

- 无向图
- adjacency matrix:邻接矩阵
- incidence matrix:$m_{ij}=\begin{cases}1&e_j\ is\ incident\ with\ v_i\\0&otherwise\end{cases}$
- isomorphic:对于图$G_1(V_1,E_1),G_2(V_2,E_2)$,若存在双射函数$f(n):V_1\rightarrow V_2$,使得任意$G_1$中相邻的$v_i,v_j$,有$G_2$中$f(v_i),f(v_j)$相邻,则$G_1,G_2$同构,函数$f$称为isomorphism
10.4 连通性
- simple path/circuit:路径或环中没有同一条边
- connected:无向图中任意两点都有路径
- cut vertices:割了就不连通的点(割点)
- cut edge/bridge:割边
- nonseparable graph:无割点的连通图
- strongly connected:有向图中,任意两点$a,b$都有路径$(a,b),(b,a)$
- weakly connected:有向图中任意两点间有路径
10.5 两个回路
- Euler circuit:包含所有边的简单环(欧拉回路)
- Euler path:包含所有边的简单路径(欧拉路径)
- 一个连通multigraph有欧拉回路当且仅当所有点度数为偶数
- 一个连通multigraph有欧拉路径但没有欧拉回路当且仅当恰好有两个点度数为奇数
- Hamilton circuit:包含所有点的简单环(哈密顿回路)
- Hamilton path:包含所有店的简单路径(哈密顿路径)
- dirac’s theorem:若所有点度数不低于$\dfrac{n}{2}$,则存在哈密顿回路
- ore’s theorem:若所有不相邻的点$u,v$有$\deg(u)+\deg(v)\ge n$,则有哈密顿回路
10.7 平面图
- planar:平面图,能在平面中画出来且没有边交错的图
- regions:平面图中,被边分割出的区域,其度数为包围它的边数,且$\sum\deg(R)=2m$
- 简单连通平面图中,$r$为区域数,$e$为边数,$v$为点数,则$r=e-v+2$(欧拉公式),$e\le 3v-6$
- 若$G$为简单连通平面图,则有一个度数不超过5的点
- 一个图是非平面图当且仅当它有一个子图与$K_{3,3}$或$K_5$同构
11 树
11.1 树树
- 树是没有简单环的连通无向图
- 一个无向图是树当且仅当任意两点间都有且仅有一条简单路径
- rooted tree:有根树
- parent:父节点
- child:子节点
- siblings:兄弟节点
- ancestors:祖先
- descendants:子孙
- leaf:叶子节点
- internal vertices:内部节点(不是叶子的节点)
- ordered rooted trees:儿子有序
- m-ary tree:m叉树
- full m-ary tree:满m叉树
- binary tree:二叉树
- subtree:子树
- 有i个内部节点的满m叉树一共有mi+1个节点和(m-1)i+1个叶子
- level:节点深度(根节点为0)
- height:树高
- balanced:所有叶子深度为h或h-1
- 高为h的m叉树最多有$m^h$个叶子
- $h\ge\lceil\log_ml\rceil$(当且仅当满且平衡等号成立)
11.2 树的应用
- binary search tree:二叉搜索树(平衡树的前身)
- prefix codes:前缀编码,任意编码不是其他编码的前缀
- Huffman coding:哈夫曼编码,为前缀编码,频率出现越高的字符编码越短。构造过程:初始有代表各个字符的若干个只有一个节点的树,每个点以字符出现频率作为权值。随后选取权值最小的两棵树,创建根节点连接两棵树,权值较大的作为根的左子树,权值较小作为右子树,合并后的新树权值为两数权值之和。不断重复此过程直到只剩下一棵树,该树上往左走为0,往右走为1,即可得到各个字符的哈夫曼编码。
- game tree:博弈树
11.3 树的遍历
- preorder traversal:先序遍历(先父后子)
- inorder traversal:中序遍历(先第一个儿子,再自己,最后其他儿子)
- postorder traversal:后序遍历(先子后父)
- Polish notation:前缀表达式
- reverse Polish notation:后缀表达式
- prefix/infix/postfix form:以先序/中序/后序遍历一个表达式的树
11.4 生成树
- spanning tree:包含所有节点且为树的子图(生成树)
- 简单图连通当且仅当其有生成树
- depth-first search:深搜
- breadth-first search:广搜
- minimum spanning tree:最小生成树(Prim和Kruskal)
后记
还是有两个词忘了,寄了
其实是太摆了







