退役前最后一个大坑,大概。
还有,关于七都的福袋活动,终于能达成我最后的心愿了(指朝奈)
前言
$\LaTeX$的向量高度不统一好难看啊。。。(模仿慎老师)
基础部分的代码是写笔记的时候直接打上去的,不保证没有手滑打错甚至可能CE,有锅的话请告诉我。
抄袭来源
来自主席的夏令营课件
https://www.cnblogs.com/lstoi/p/9791654.html
https://www.cnblogs.com/shzr/p/12014963.html
基础
终于(算是)整理完了。。。
精度问题
计算几何的运算中会出现很大大大大的精度误差,要重新定义实数的比较运算:
const double eps = 1e-9;
inline int cmp(double a,double b){return fabs(a-b)<eps?0:a-b<-eps?-1:1;}//0:a==b;-1:a<b;1:a>b
后来发现了一种绝妙的cmp写法:
inline int cmp(double a,double b){return (a-b>eps)-(a-b<-eps);}
你品,你细品。
点/向量
定义及四则运算
必修二基础知识。。。
struct point{
double x,y;
point(double X=0,double Y=0){x=X,y=Y;}
point operator + (point a){return point(x+a.x,y+a.y);}
point operator - (point a){return point(x-a.x,y-a.y);}
point operator * (double a){return point(x*a,y*a);}
point operator / (double a){return point(x/a,y/a);}
};
以下均以$\vec{a},\vec{b}$举例,坐标分别为$(x_a,y_a),(x_b,y_b)$
点乘和叉乘
点乘($dot\ product$)不说了,以下用$\vec{a}\cdot \vec{b}$表示点乘。
$\vec{a}\cdot\vec{b}=|a||b|\cos\langle\vec{a},\vec{b}\rangle=x_ax_b+y_ay_b$
叉乘($cross\ product$)用$\vec{a}\times\vec{b}$表示。
$a\times b=|a||b|\sin\langle\vec{a},\vec{b}\rangle=x_ay_b-x_by_a$
其含义简单地说,就是平行四边形定则中那个平行四边形(ABDC)的有向面积。$\vec{a}$在$\vec{b}$顺时针方向为正,否则为负。
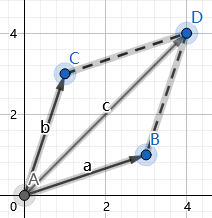
叉乘不满足结合律和交换律(交换时要取反:$\vec{a}\times\vec{b}=-\vec{b}\times\vec{a}$),但满足分配律。
inline double dot(point a,point b){return a.x*b.x+a.y*b.y;}
inline double cross(point a,poit b){return a.x*b.y-a.y*b.x;}
点乘可以判断向量夹角情况:钝角小于$0$,锐角大于$0$。
叉乘可以用于判断向量方向关系,大于$0$则$\vec{a}$在$\vec{b}$的顺时针方向,等于$0$共线,否则为逆时针。
夹角
计算$\vec{a}$和$\vec{b}$的夹角。
$\vec{a}\cdot\vec{b}=|a||b|\cos\langle\vec{a},\vec{b}\rangle$
$\vec{a}\times\vec{b}=|a||b|\sin\langle\vec{a},\vec{b}\rangle$
$\tan\langle\vec{a},\vec{b}\rangle=\dfrac{\sin\langle\vec{a},\vec{b}\rangle}{\cos\langle\vec{a},\vec{b}\rangle}=\dfrac{\vec{a}\times\vec{b}}{\vec{a}\cdot\vec{b}}$
inline double angle(point a,point b){return atan2(cross(a,b),dot(a,b));}
注:atan2传入两个参数$y$和$x$,返回弧度制,范围$(-\pi,\pi]$。
旋转
将幅角为$\alpha$的$\vec{a}$旋转$\beta$度。
$\vec{a}$一定能表示成$k(\cos\alpha,\sin\alpha)$。把$(\cos\alpha,\sin\alpha)$转过去再乘上$k$。
即$k(\cos(\alpha+\beta),\sin(\alpha+\beta))=k(\cos\alpha\cos\beta-\sin\alpha\sin\beta,\sin\alpha\cos\beta+\cos\alpha\sin\beta)=(x_a\cos\beta-y_a\sin\beta,y_a\cos\beta+x_a\sin\beta)$
inline point rotate(point a,double b){return point(a.x*cos(b)-a.y*sin(b),a.y*cos(b)+a.x*sin(b));}
其他
inline double abs2(point a){return a.x*a.x+a.y*a.y}//模长的平方
inline double abs(point a){return sqrt(abs2(a));}//模长
inline double unit(point a){return a/abs(a);}//单位向量
inline double dis(point a,point b){return abs(a-b);}//距离
inline double angle(point a){return atan2(a.y,a.x);}//幅角,也能用来求夹角
直线/线段
定义
两点确定一条直线。
struct line{
point a,b;
line(point A=point(0,0),point B=point(0,0)){a=A,b=B;}
}
点线位置关系
点在直线上
判断$\overrightarrow{PA}$、$\overrightarrow{PB}$与直线围成的三角形面积是否为$0$,即$\overrightarrow{PA}\times\overrightarrow{PB}=0$
inline bool locate(point a,line b){return cmp(cross(b.a-a,b.b-a),0.0)==0;}
点在线段上
和直线一样,但要判断坐标范围:
inline bool in(double a,double b,double c){return cmp(a,b)==0||cmp(a,c)==0||cmp(a,b)!=cmp(a,c);}
inline bool in(point a,line b){return in(a.x,b.a.x,b.b.x)&&in(a.y,b.a.y,b.b.y);}
线线位置关系
平行
叉乘等于$0$。
inline bool par(line a,line b){return cmp(cross(a.a-a.b,b.a-b.b),0.0)==0;}
垂直
点乘等于$0$。
inline bool ver(line a,line b){return cmp(dot(a.a-a.b,b.a-b.b),0,0)==0;}
直线交点
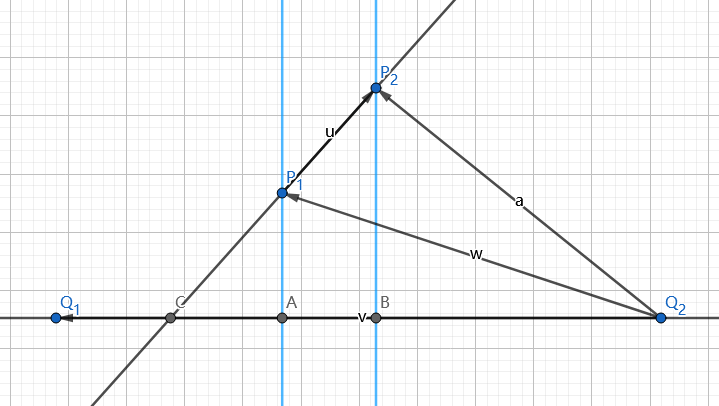
直线$P_1P_2$与$Q_1Q_2$交点为$C$。作$P_1A\perp Q_1Q_2,P_2B\perp Q_1Q_2$,垂足分别为$A,B$。连接$Q_2P_1,Q_2,P_2$。
由三角形面积公式得$\dfrac{|\overrightarrow{P_1A}|}{|\overrightarrow{P_2B}|}=\dfrac{\overrightarrow{Q_2P_1}\times\overrightarrow{Q_2Q_1}}{\overrightarrow{Q_2P_2}\times\overrightarrow{Q_2Q_1}}$
记$x=\overrightarrow{Q_2P_1}\times\overrightarrow{Q_2Q_1}$,$y=\overrightarrow{Q_2P_2}\times\overrightarrow{Q_2Q_1}$。
由相似得$\dfrac{|\overrightarrow{P_1C}|}{|\overrightarrow{P_2C}|}=\dfrac{|\overrightarrow{P_1A}|}{|\overrightarrow{P_2B}|}=\dfrac{x}{y}$
因为这几组模长的比例关系都是平行向量之间的比较,可以把绝对值去掉:
$\dfrac{\overrightarrow{P_1C}}{\overrightarrow{P_2C}}=\dfrac{x}{y}$
$\overrightarrow{P_2P_1}=\overrightarrow{P_2C}-\overrightarrow{P_1C}$
解方程:$\overrightarrow{P_1C}=\dfrac{x}{y-x}\overrightarrow{P_2P_1}$
$\vec{c}=\vec{p_1}+\overrightarrow{P_1C}$
inline point inter(line a,line b){
double x=cross(a.a-b.b,b.b-b.a),y=cross(a.b-b.b,b.b-b.a);
return a.a+(a.a-a.b)*x/(y-x);
}
后来发现太丑了换了一种求法:
首先,除了用两个点,直线还有一种表示方式:一个端点和方向向量。实际上这个方向向量就是两端点相减。
假设直线$(P,\vec{a}),(Q,\vec{b})$交点为$C$。
显然,我们可以用$P+t\vec{a}$来表示一个在直线上的点。
设$C=P+t_1\vec{a}=Q+t_2\vec{b}$。
大力列方程:
$\begin{cases}x_C=x_P+t_1x_a=x_Q+t_2x_b\\y_C=y_P+t_1y_a=y_Q+t_2t_b\end{cases}$
大力化式子:
$t_1=\dfrac{x_by_P-x_Py_b+x_Qy_b-x_by_Q}{x_ay_b-x_by_a}$
大力叉乘:
$t_1=\dfrac{\vec{b}\times\vec{p}+\vec{q}\times\vec{b}}{\vec{a}\times\vec{b}}=\dfrac{\vec{b}\times(\vec{p}-\vec{q})}{\vec{a}\times\vec{b}}$
inline point inter(line a,line b){
point A=a.b-a.a,B=b.b-b.a;
return a.a+A*cross(B,a.a-b.a)/cross(A,B);
}
线段交点
和直线一样,但是也要判断一下求出来的点是否在线段上。
其他
投影
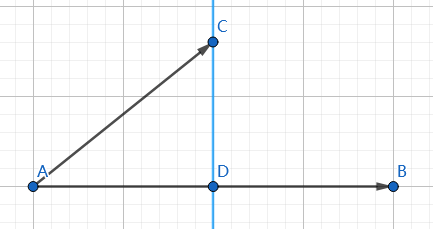
点$C$在$\overrightarrow{AB}$上的投影为$D$。
$\overrightarrow{AC}\cdot\overrightarrow{AB}=|\overrightarrow{AD}||\overrightarrow{AB}|$
$|\overrightarrow{AD}|=\dfrac{\overrightarrow{AC}\cdot\overrightarrow{AB}}{|\overrightarrow{AB}|}$
转化$\overrightarrow{AD}$为其模长乘单位向量:
$\overrightarrow{AD}=|\overrightarrow{AD}|\dfrac{\overrightarrow{AB}}{|\overrightarrow{AB}|}=\dfrac{(\overrightarrow{AB}\cdot\overrightarrow{AC})\overrightarrow{AB}}{|\overrightarrow{AB}|^2}$
$\vec{d}=\vec{a}+\overrightarrow{AD}$
inline point project(point a,line b){
point AB=b.b-b.a;
return b.a+AB*dot(AB,a-b.a)/abs2(AB);
}
点到直线距离
投个影求两点距离即可。
inline double dis(point a,line b){
point p=project(a,b);
return dis(a,p);
}
点到线段距离
同上,判断一下投影是否在线段上,不在的话取两端点距离最小值。
直线到直线距离
先判断是否平行,不平行距离为$0$;否则任取一点计算到另一条直线的距离。
inline double dis(line a,line b){
if(!par(a,b))return 0;
return dis(a.a,b);
}
线段到线段距离
判断平行,不平行的话要把不属于同一线段的端点距离都算一遍,取最小值。
多边形
定义
vector存储即可。
typedef vector<point> polygon;
为了方便下面计算,要求按逆时针方向存储各顶点。
面积
先考虑原点在多边形内部的情况:
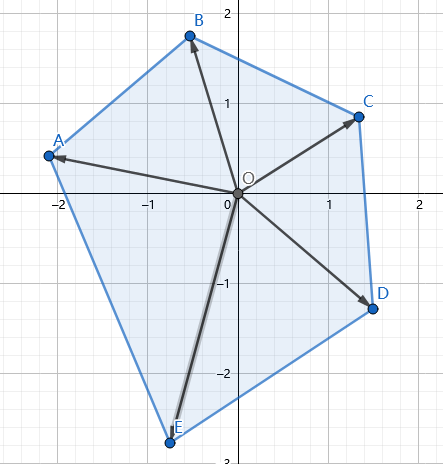
把多边形分成若干个三角形,容易看出每个三角形的面积就是相邻两点叉乘的一半。
如果原点不在多边形内部呢?
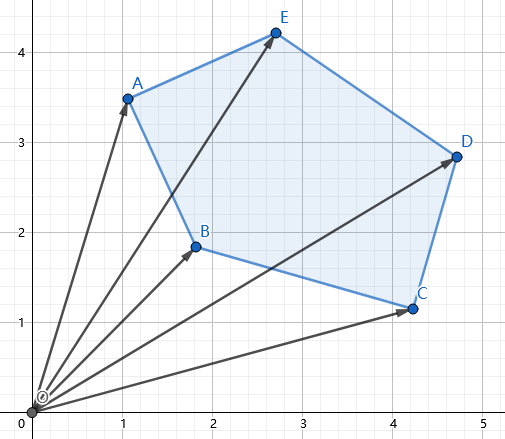
在计算下面$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$之间的叉乘时,因为和上面的方向相反,正好把多出来的白色部分减掉了,所以一样适用。
顺便发现了一种不用取模或特判的循环方法:
inline double area(const polygon &a){
double ans=0;
for(register int i=0,j=a.size()-1;i<a.size();j=i++)ans+=cross(a[j],a[i]);
return ans/2;
}
点在多边形内部
网上基本都是水平向左引一条射线判断与多边形交点数的奇偶。但这样还要处理过顶点之类的特殊情况。在「算法竞赛·入门经典」上看到一种不用特判的方法。
水平向右引一条射线,正穿过一条边加1,反穿过一条边减1,最后如果和为$0$,说明不在多边形上。
判断正穿和反穿:
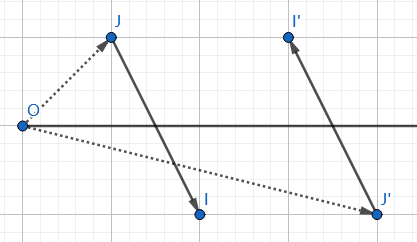
- 左边情况:$\overrightarrow{OJ}\times\overrightarrow{JI}<0,y_O\in[y_I,y_J]$
- 右边情况:$\overrightarrow{OJ’}\times\overrightarrow{OI’}>0,y_O\in[y_{J’},y_{I’}]$。
inline int contain(point a,polygon &b){
int cnt=0;
for(register int i=0,j=b.size()-1;i<b.size();j=i++){
if(locate(a,line(b[i],b[j])))return -1;//在多边形边界上
if(cmp(a.y,b[j].y)==cmp(a.y,b[i].y))continue;
double k=cross(b[j]-a,b[i]-b[j]);
if(k<0&&cmp(a.y,b[i].y)>=0)++cnt;
else if(k>0&&cmp(a.y,b[j].y)>=0)--cnt;
}
return (bool)cnt;
}
重心
直接背过吧
分成若干三角形,记$S_i$为第$i$个三角形的有向面积,$(x_i,y_i)$为第$i$个三角形的重心。
$x=\dfrac{\sum S_ix_i}{\sum S_i},y=\dfrac{\sum S_iy_i}{\sum S_i}$
三角形$(x_1,y_1)-(x_2,y_2)-(x_3,y_3)$的重心:
$\left(\dfrac{x_1+x_2+x_3}{3},\dfrac{y_1+y_2+y_3}{3}\right)$
inline point center(const polygon &a){
double S=0.0,x=0.0,y=0.0;
for(register int i=0,j=a.size()-1;i<a.size();j=i++){
double s=cross(a[i],a[j]);
S+=s,x+=s*(a[i].x+a[j].x)/3,y+=s*(a[i].y+a[j].y)/3;
}
return point(x/S,y/S);
}
圆
定义
圆心与半径。
struct circle{
point c;
double r;
circle(point C=point(0,0),double R=0){c=C,r=R;}
};
三点定圆
众所周知,不共线的三个点确定一个圆。
用平面几何可以搞。做两条中垂线算交点即为圆心,算个距离就是半径。
但这样涉及到旋转、交点和距离,比较繁琐,常数和精度不够优秀。考虑用解析几何。
设三个点分别为$(x_1,y_1),(x_2,y_2),(x_3,y_3)$,圆的圆心为$(x_0,y_0)$,方程为$(x-x_0)^2+(y-y_0)^2=r^2$。
直接把三个点带进去,大力搞方程组。解方程的过程太复杂直接说结论了:
令
$a=x_1^2-x_2^2+y_1^2-y_2^2$
$b=x_2^2-x_3^2+y_2^2-y_3^2$
$c=x_1-x_2$
$d=y_1-y_2$
$e=x_2-x_3$
$f=y_2-y_3$
$x_0=\dfrac{af-bd}{2(cf-de)}$
$y_0=\dfrac{bc-ae}{2(cf-de)}$
最后带回去算$r$即可。
circle(point A,point B,point C){
#define sqr(x) ((x)*(x))
double a=sqr(A.x)-sqr(B.x)+sqr(A.y)-sqr(B.y),b=sqr(B.x)-sqr(C.x)+sqr(B.y)-sqr(C.y),_c=A.x-B.x,d=A.y-B.y,e=B.x-C.x,f=B.y-C.y,m=2*(_c*f-d*e);
c=point((a*f-b*d)/m,(b*_c-a*e)/m);
r=sqrt(sqr(A.x-c.x)+sqr(A.y-c.y));
#undef sqr
}
切线
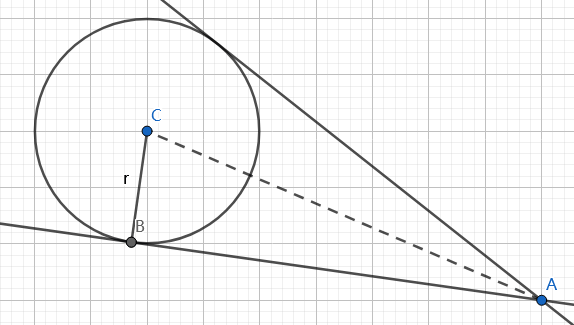
根据点到圆心距离和半径用反三角函数能算出来$\left\langle\overrightarrow{AC},\overrightarrow{AB}\right\rangle$,把$\overrightarrow{AC}$转一下即可。
inline line tangent(point a,circle b){
double d=dis(a,b.c);
return line(rotate(b.c-a,asin(b.r/d))+a,a);
//另一条切线就是-asin
}
圆和直线的交点
比较圆心到直线的距离和半径的关系判断有没有交。
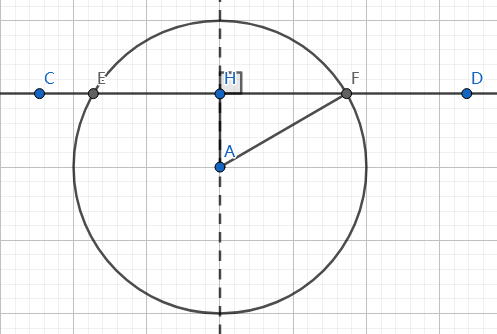
一看就是有垂径定理了,作$A$在$CD$上的投影$H$。
根据勾股定理,$|HF|=\sqrt{|AF|^2-|AH|^2}=\sqrt{r^2-|AH|^2}$。
$\overrightarrow{HF}=|HF|\dfrac{\overrightarrow{CD}}{|CD|}$
$\vec{f}=\vec{h}+\overrightarrow{HF}$
inline point inter(line a,circle b){
point h=project(b.c,a);
return h+(a.b-a.a)*sqrt((b.r*b.r-abs2(b.c-h))/abs2(a.b-a.a));
//另一个交点就是h-...
}
圆和圆的交点
比较圆心的距离和半径之和的关系判断有没有交。
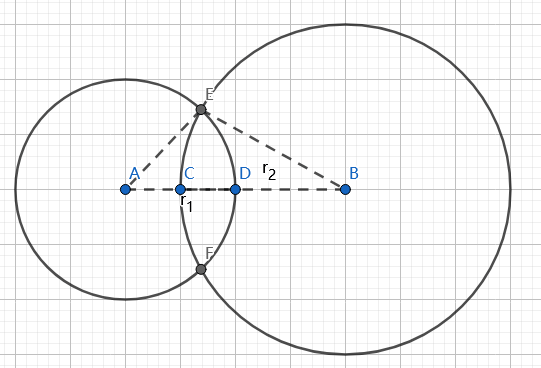
根据余弦定理:
$|BE|^2=|AE|^2+|AB|^2-2|AB||AE|\cos\left\langle\overrightarrow{AB},\overrightarrow{AE}\right\rangle$
$\left\langle\overrightarrow{AB},\overrightarrow{AE}\right\rangle=\arccos\left(\dfrac{|AE|^2+|AB|^2-|BE|^2}{2|AB||AE|}\right)=\arccos\left(\dfrac{r_1^2-r_2^2+|AB|^2}{2r_1|AB|}\right)$
旋转一下$\overrightarrow{AB}$,乘上$\dfrac{|AE|}{|AB|}$得到$\overrightarrow{AE}$。
inline point inter(circle a,circle b){
double d=dis(a.c,b.c);
return rotate(b.c-a.c,acos((a.r*a.r-b.r*b.r+d*d)/(2.0*a.r*d)))*a.r/d+a.c;
//另一个交点就是-acos
}
外公切线
GeoGebra画不了公切线将就着看吧
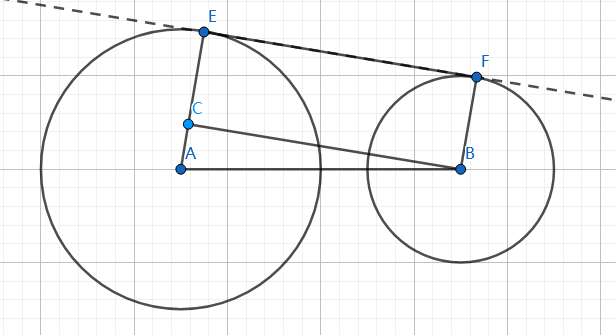
作$BC\perp AE$于$C$。
用反三角函数能得到$\left\langle\overrightarrow{AB},\overrightarrow{AE}\right\rangle$,旋转$\overrightarrow{AB}$,乘上$\dfrac{r_1}{|AB|}$就能得到$\overrightarrow{AE}$,进而得到$\vec{e}$。
同理能得出$\vec{f}$。
const double pi = acos(-1);
inline line ex_common_tangent(circle a,circle b){
point AB=b.c-a.c;
double d=abs(AB),an=acos((a.r-b.r)/d);
return line(point(a.c+rotate(AB,an)*a.r/d),point(b.c+rotate(a.c-b.c,an-pi)*b.r/d));
//把旋转角度都取反得到另一条外公切线
}
内公切线
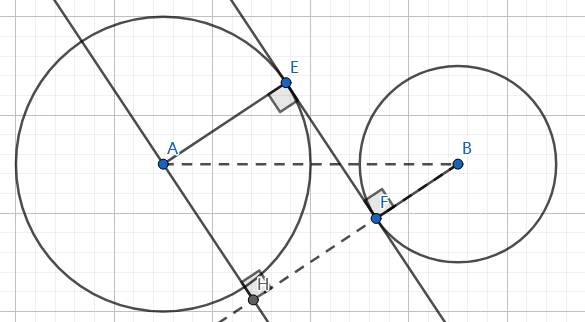
和外公切线差不多。
作$AH\perp BF$延长线于$H$。
用反三角函数得到$\left\langle\overrightarrow{BA},\overrightarrow{BH}\right\rangle=\left\langle\overrightarrow{AB},\overrightarrow{AE}\right\rangle$,把$\overrightarrow{AB}$转到$\overrightarrow{AE}$乘上$\dfrac{r_1}{|AB|}$得到$\overrightarrow{AE}$,进而得到$\vec{e}$,同理得到$\vec{f}$。
代码和外公切线的区别只有a.r-b.r改成a.r+b.r和an-pi改成an。
inline line in_common_tangent(circle a,circle b){
point AB=b.c-a.c;
double d=abs(AB),an=acos((a.r+b.r)/d);
return line(point(a.c+rotate(AB,an)*a.r/d),point(b.c+rotate(a.c-b.c,an)*b.r/d));
//旋转角度都取反得到另一条内公切线
}
二维凸包
凸包就是平面上有一堆点,把最外围的点连成一个凸多边形,框起来这些点。
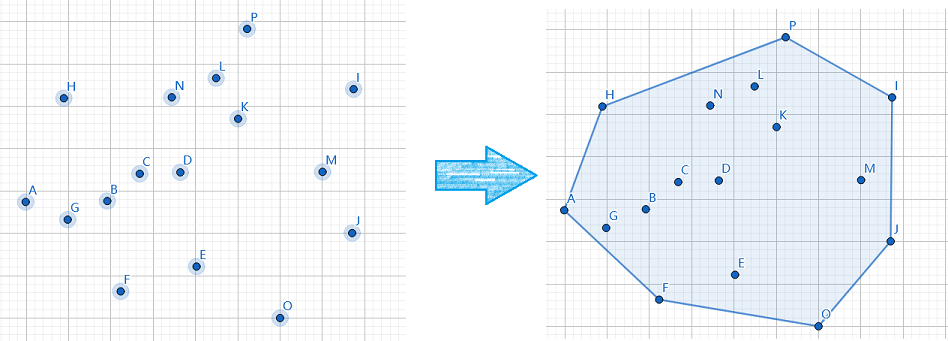
这里是一种不正经的方法求凸包说不定哪天就翻车了,想学正经的Andrew算法的另寻大佬吧。
如果学过斜率优化$DP$的话甚至可以自己$yy$出来。对这些点求一个上凸壳和一个下凸壳拼起来即可。
上凸壳就是维护一个相邻点构成的直线斜率递减的点集,下凸壳则是递增的。不过这里我们还有chuan新的判断方式:计算差积判断方向。
和斜率优化一样,以横坐标为第一关键字、纵坐标为第二关键字排序,用单调栈维护凸壳。
找上凸壳的时候可以倒着再求一遍下凸壳,避免重新排序。
之后我们会发现一个问题:上凸壳和下凸壳的点可能会有交集。
这样常数大了,有的时候还会导致求某些东西的时候出锅。需要再对凸包上的点去重。
struct point{
double x,y;
point(double X=0.0,double Y=0.0){x=X,y=Y;}
point operator + (const point &a){return point(x+a.x,y+a.y);}
point operator - (const point &a){return point(x-a.x,y-a.y);}
bool operator < (const point &a)const{return x==a.x?y<a.y:x<a.x;}
bool operator != (const point &a){return x!=a.x||y!=a.y;}
}p[maxn],sta[maxn],u[maxn];
typedef vector<point> polygon;
int top;
polygon v;
inline int cmp(double a,double b){return fabs(a-b)<eps?0:a-b>eps?1:-1;}
inline double abs(const point &a){return a.x*a.x+a.y*a.y;}
inline double abs2(const point &a){return sqrt(abs(a));}
inline double dis(point a,point b){return abs2(a-b);}
inline double cross(const point &a,const point &b){return a.x*b.y-a.y*b.x;}
int main(){
int n=read(),cnt=0;
double ans=0.0;
for(register int i=1;i<=n;++i)scanf("%lf%lf",&p[i].x,&p[i].y);
sort(p+1,p+1+n);
for(register int i=1;i<=n;++i){
while(top>1&&cmp(cross(p[i]-sta[top],sta[top]-sta[top-1]),0)>=0)--top;
sta[++top]=p[i];
}
for(register int i=1;i<=top;++i)u[i]=sta[i];
cnt=top,top=0;
for(register int i=n;i;--i){
while(top>1&&cmp(cross(p[i]-sta[top],sta[top]-sta[top-1]),0)>=0)--top;
sta[++top]=p[i];
}
for(register int i=1;i<=top;++i)u[++cnt]=sta[i];
for(register int i=1,j=cnt;i<=cnt;j=i++)if(u[i]!=u[j])v.push_back(u[i]);
for(register int i=0,j=v.size()-1;i<v.size();j=i++)ans+=dis(v[i],v[j]);
printf("%.2lf\n",ans);
}
旋转卡壳
考虑怎么找到一个点的最远点。
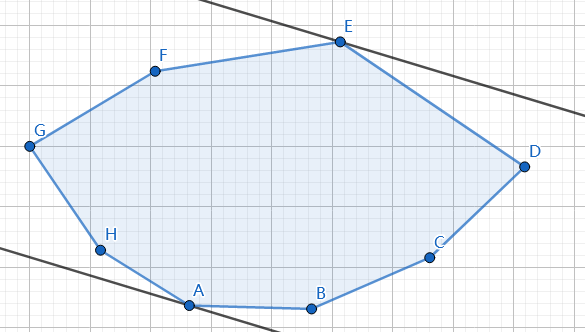
过点$A$作一条直线(不能与凸包内有交),再过另一个点作一条平行线,使两条直线距离最大,这个点($E$)就是最远点了。这两个点就叫对踵点。
不过随便作一条直线的话好像不太好找,让这条直线过凸包的一条边:
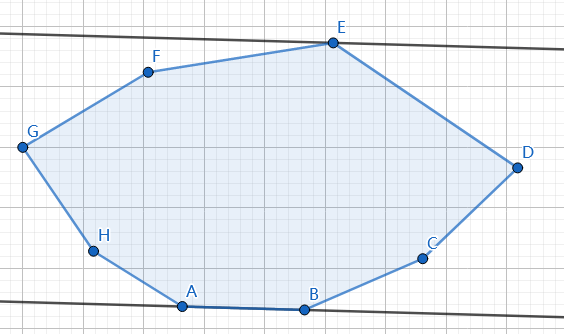
这时通过计算三角形的面积,即通过叉乘,就能判断平行线之间的距离了:
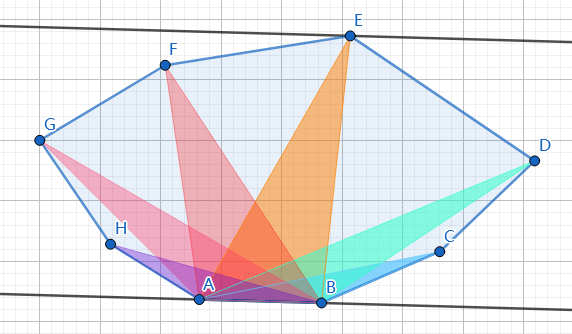
而且,观察一下会发现,这个面积是一个单峰函数。
于是依次遍历每条边,让最远点跟着动。剽张gif:
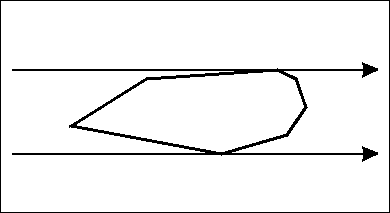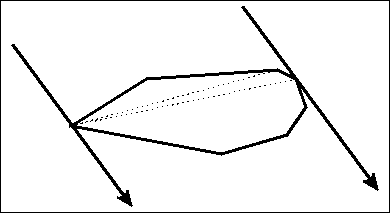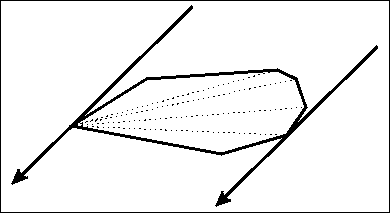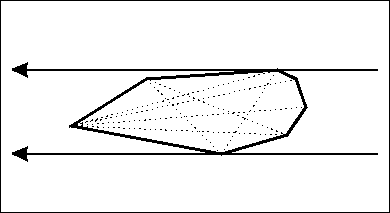
代码很简短:
if(c.size()==2){printf("%d\n",abs2(c[0]-c[1]));return 0;}//特判两个点
int k=1,ans=0;
for(register int i=0,j=c.size()-1;i<c.size();++i,j=i++){
while(cross(c[i]-c[j],c[k]-c[j])<cross(c[i]-c[j],c[(k+1)%c.size()]-c[j]))k=(k+1)%c.size();
ans=max(max(ans,abs2(c[i]-c[j])),max(abs2(c[k]-c[i]),abs2(c[k]-c[j])));
}
printf("%d\n",ans);
半平面交
什么是半平面交?
一条有向直线左侧的平面称为半平面。顾名思义,半平面交就是若干条有向直线的半平面的交集。
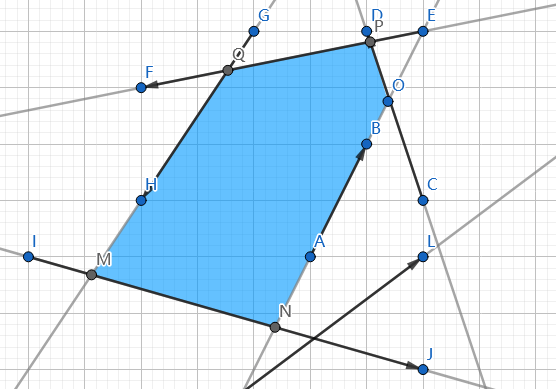
朴素的求法是$O(n^2)$的,维护当前的半平面交,枚举直线切割半平面交,如果能缩小交集就加入,再删去无用直线。
定义一条有向直线的极角为其与$x$轴正半轴夹角。
优化朴素算法,要先按极角排序本来求凸包要用极角排序的,但是我求凸包的方法太鬼畜了结果拖到这里
用双端队列维护若干条直线表示当前半平面交。加入一条直线,分别在队尾和队首把无用的直线弹掉:
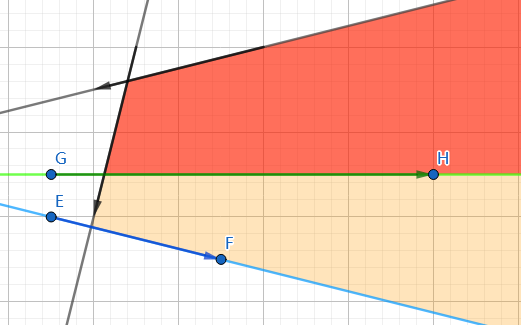
加入绿色直线后,蓝色直线就无用了。得到判断方式为:只要队尾和队尾前一条直线的交点在新直线右侧(判断左右用叉乘),队尾就无用。队首同理。
把新直线压到队尾。最后双端队列中相邻元素求交点得到的凸多边形就是半平面交。
再有两个细节:
一个是极角排序时,如果有几条直线极角相同,要仅保留最靠左的直线。不然求交点会炸。
另一个是求完半平面交之后,双端队列里可能会出现这种东西:
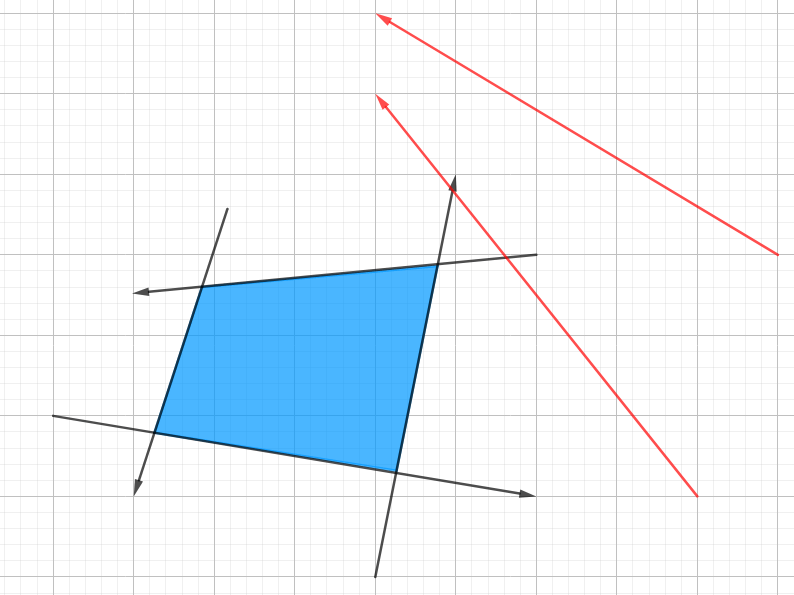
两条红色直线是最后加入双端队列的,但它们都没有用。而且如果模拟一下上面的过程,这种直线的出现是合情合理的。
如果再加一条直线呢?
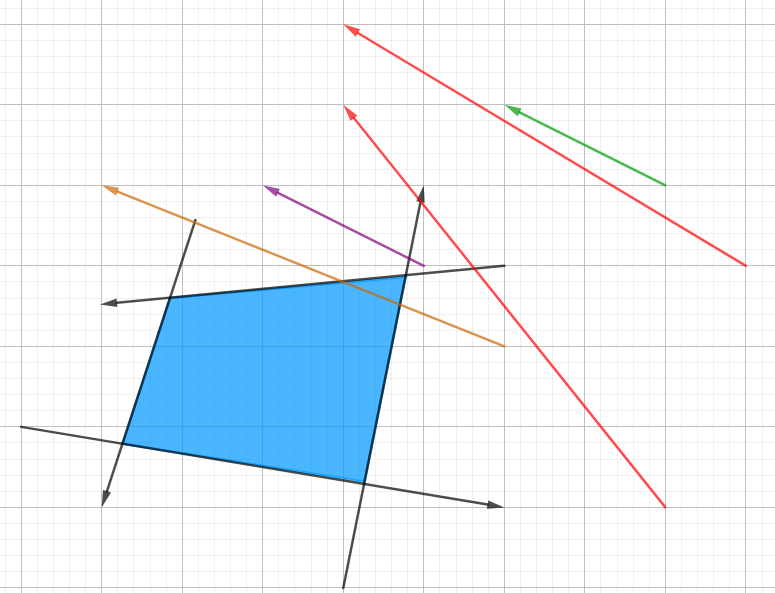
如果是绿/紫色位置(新直线无用),要么红色直线被判为无用弹出,要么只把新直线压进去;如果是棕色位置(新直线有用),红色直线必定被弹出。
所以这种直线一定都堆积在队尾。求完半平面交后,检查一下队尾两条直线交点和队首直线的关系即可。
复杂度瓶颈在排序,$O(n\log n)$的。
inline bool mmp(line &a,line &b){
int k=cmp(angle(a),angle(b));
if(!k)return cmp(cross(b.b-a.a,b.a-a.a),0)==-1;
return k==-1;
}
inline bool judge(point &a,line &b){return cmp(cross(b.b-a,b.a-a),0)==1;}
point p[maxn];
line l[maxn],q[maxn];
polygon v;
int main(){
int n=read(),h=1,t=0,cnt=0;
while(n--){
v.clear();
int m=read();
point p;
while(m--)p.x=read(),p.y=read(),v.push_back(p);
for(register int i=0,j=v.size()-1;i<v.size();j=i++)l[++cnt]=line(v[j],v[i]);
}
sort(l+1,l+1+cnt,mmp);
for(register int i=1;i<=cnt;++i){
if(i!=1&&!cmp(angle(l[i]),angle(l[i-1])))continue;
while(t-h>=1&&judge(p[t],l[i]))--t;
while(t-h>=1&&judge(p[h+1],l[i]))++h;
q[++t]=l[i];
if(t-h>=1)p[t]=inter(q[t],q[t-1]);
}
v.clear();
while(t-h>=1&&judge(p[t],q[h]))--t;
v.push_back(inter(q[h],q[t]));
for(register int i=h+1;i<=t;++i)v.push_back(p[i]);
printf("%.3lf\n",area(v));
}
板子的性质比较好,没有特殊情况。
如果半平面交不是个封闭图形呢?
强行用一个极大的矩形规定坐标范围(超过题目给定坐标范围),加进半平面交里即可。
如果半平面交是空集呢?
此时队列元素个数不超过2。因为前面用一个大矩形框了起来,所以只要存在半平面交,一定有至少三条直线。
还有一道双倍经验。实际上这样能无死角看到整个多边形的区域就是半平面交,被称为多边形的核。
最小圆覆盖
给出平面上的$n$个点,求一个最小的圆使其覆盖所有的点。
这个要用随机增量法。
不难发现一个结论:如果点集$S$的最小覆盖圆没有覆盖到$P$,则$P$一定在$S\cup\{P\}$的最小覆盖圆上。
根据这个,我们可以得到一个复杂度不靠谱的解法:
- 遍历一遍点集,维护前$i-1$个点的最小覆盖圆作为当前答案(记为$ans$)
- 如果$P_i$没有被$ans$覆盖,则根据上面的结论,更新$ans$为以$P_i$为圆心、半径为$0$的圆,遍历前$i-1$个点(假设当前遍历到了$P_j$)
- 如果$P_j$没有被$ans$覆盖,更新$ans$为以$P_i,P_j$中点为圆心,半径为$\frac{dis(P_i,P_j)}{2}$的圆,遍历前$j-1$个点(假设当前遍历到了$P_k$)
- 如果$P_k$没有被$ans$覆盖,此时我们就得到了$P_i,P_j,P_k$三个位于当前点集最小覆盖圆上的点,三点定圆更新$ans$
乍一看是$O(n^3)$的,既然是随机增量法,先random_shuffle打乱点集。
- 第一层遍历:根据三点定圆,$P_i$有$\frac{3}{i}$的概率在前$i$个点的最小覆盖圆上,进入第二层遍历。
- 第二层遍历:遍历到$P_j$时,实际上是在求$\{P_i\}\cup\{P_x|x\le j\}$的最小覆盖圆,点集大小为$j+1$,$P_j$有$\frac{3}{j}$的概率被选中,进入第三层遍历。
- 第三层遍历的复杂度显然是点集大小的。
于是得到:
$T_1(n)=O(n)+\sum\limits_{i=1}^n\dfrac{3}{i}T_2(i)$
$T_2(n)=O(n)+\sum\limits_{i=1}^n\dfrac{3}{i}T_3(i)$
$T_3(n)=O(n)$
所以期望复杂度是$O(n)$的。
point p[maxn];
circle ans;
inline bool contain(point &a,circle &b){return cmp(abs2(a-b.c),b.r*b.r)<=0;}
int main(){
int n=read();
for(register int i=1;i<=n;++i)scanf("%Lf%Lf",&p[i].x,&p[i].y);
random_shuffle(p+1,p+1+n);
for(register int i=1;i<=n;++i){
if(!contain(p[i],ans)){
ans=circle(p[i],0);
for(register int j=1;j<i;++j)
if(!contain(p[j],ans)){
ans=circle((p[i]+p[j])/2,dis(p[i],p[j])/2);
for(register int k=1;k<j;++k)
if(!contain(p[k],ans))ans=circle(p[i],p[j],p[k]);
}
}
}
printf("%.10Lf\n%.10Lf %.10Lf\n",ans.r,ans.c.x,ans.c.y);
}
水题
信用卡凸包
显然凸包上的圆弧加起来是个整圆,对所有圆心求凸包即可。
最大土地面积
显然答案一定是在凸包上的四个点。
枚举对角线,然后四边形的面积就被分成两个三角形。和旋转卡壳一样,这两个三角形的面积都是单峰函数,于是再维护两个指针跟着对角线走即可。$O(n^2)$可过。
最小矩形覆盖
先求个凸包。
猜一下结论,矩形的一条边一定和凸包的一条边重合。
感觉挺对的,那我们枚举这条边就行了,其对边显然过对踵点。而邻边也一定过凸包上的点,维护一下这两个点,旋转卡壳的时候跟着动就行了。
计算面积和求矩形投影旋转啥的就行了。
射箭
二分答案。
观察限制$ax^2+bx\in [y_1,y_2]$,化简为$ax+b\in [\frac{y_1}{x},\frac{y_2}{x}]$。
把$a$看作自变量,$b$看作因变量,那么形如$ax+b\le c$或$ax+b\ge c$实际上是一个半平面。判断一下半平面交是否为空即可。
我们需要用一个极大的矩形框起来坐标系,同时由于抛物线在第一象限,有一个潜在的条件$a\lt0,b\gt0$,所以选择第二象限的矩形。
提前排好序就能$O(n\log n)$了。
最后,为丧心病狂卡精度卡常的出题人献上祝福:
#define double long double
const double eps = 1e-18;
const double inf = 1e10;
数矩形
可以证明,矩形个数上界为$O(n^{2.5})$。
根据矩形对角线等长同中点,对$C_n^2$条线段排序暴力枚举即可。
瞭望塔
先求出来多边形的核。然后是一个结论:瞭望塔的位置一定在半平面交或地形的一个端点上。
证明很简单,把半平面交和地形的端点抠出来,横坐标相邻的放一块,截取中间的半平面交和地形,一定是上下两条线段。
分类讨论一下,无非是斜率一个大一个小。如果上面的斜率大,在线段上任意一点一定不如左端点;反之为右端点。
赛车
很裸的半平面交。由于时间是正数,要用一个$y$轴负半轴方向的向量限制一下。
小凸想跑步
信号增幅仪
把$x$轴逆时针旋转$a^\circ$(也就是把所有点旋转$-a^\circ$),再把所有点的横坐标缩小至$\frac{1}{p}$倍,就是最小圆覆盖了。







