neb e denoe rsdi gWeiFielb?in
世界上最无聊的事之一——造一个连自己也不会破译的密码。
前言
真的,不要尝试破译上面那个密码,你会爆炸的
决策单调性是一类优化动态规划的算法。
我也没想到生成函数这么快就结束了,干脆垫上一些小算法后开计算几何吧。
抄袭来源
https://www.luogu.com.cn/problemnew/solution/P1912
某网课
决策单调性
定义
如果我们有一个$DP$的式子:$f(i)=\min\limits_{j<i}\{f(j)+w(j,i)\}$
其中$w(j,i)$是一个与$i,j$有关的二元函数。而且这个$w(j,i)$搞不了单调队列或斜率优化。
但是,如果我们通过打表或证明发现决策点是单调不降的($f$值不一定单调),这个$DP$就满足决策单调性。
形式化地说,记$p_i$为$f(i)$的决策点(即$p_i$是使$f(j)+w(j,i)$最小的那个$j$),则$\forall i>j,p_i\ge p_j$。
这样我们就可以根据决策单调性优化$DP$。
如何证明
怎么优化下面讲。先说一下如何证明。(以上面的$\min$方程为例,$\max$倒过来就好啦)
直接输出决策点打表是一个好办法,然后再写一个决策单调性优化$DP$和暴力拍。
而严谨的证明可以用四边形不等式。(以下只给出结论,结论和四边形不等式性质的证明我太菜了不会,还请自行搜索)
四边形不等式:如果$\forall a<b<c<d,w(a,c)+w(b,d)\le w(a,d)+w(b,c)$(相交优于包含)且$w(a,d)\ge w(b,c)$(大区间比其子区间权值大),称为四边形不等式,此时满足决策单调性。
这个式子看起来不太好用来证明,还有一个性质:
如果$\forall a<b,w(a,b)+w(a+1,b+1)\le w(a,b+1)+w(a+1,b)$,则满足四边形不等式。
其实还是“相交优于包含”,只是把区间放缩了一下,更容易证明了。
还有一种更直观更好用的证明方法:
考虑决策单调性的实质:为什么会出现决策单调性?
决策点单调不降,换句话说,如果$i$有两个决策点$j,k(k<j)$,只要$j$优于$k$,那么在之后$i+1,i+2\dots$的决策中,$k$就再也没有反超的机会了。
$k$怎么着就反超不了$j$了?随着$i$的增加,$w(k,i)$的增长速度比$w(j,i)$快。
所以只要证明自变量为$i$的函数$w(j,i)$满足任意$k<j$,$w(k,i)$增长速度比$w(j,i)$快即可。
你会发现这实质上就是四边形不等式,但从决策单调性的角度上理解更直观了。
优化
一般有两种优化方式——二分和分治。
二分
解法
设$f(i)$为前$i$句话的最小代价,$sum_i$为$\sum\limits_{j\le i}len(s_j)+1$。
$DP$方程显然:$f(i)=\min\limits_{j<i}\{f(j)+|sum_i-sum_j-L-1|^P\}$。
打表可以发现决策单调性,尝试证明一下:
$w(j,i)$就是$|sum_i-sum_j-L-1|^P$。
假设有$k<j$,现在要证明$w(k,i)$增长速度比$w(j,i)$快,即$|sum_i-sum_k-L-1|^P$增长速度比$|sum_i-sum_j-L-1|^P$快。
令$p=-sum_k-L-1,q=-sum_j-L-1$,显然$p>q$。
尝试画出$w(k,i)$和$w(j,i)$的图象:
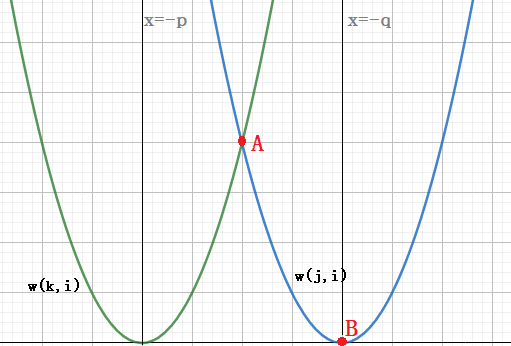
这里只画了$P=2$的情况。但只要$P>1$,$|x+c|^p$的图象就有这些性质:
- 关于$x=-c$对称
- 在对称轴左侧单调递减,右侧单调递增
- 离对称轴越远,下降/增长速率越快
分类讨论:
- 当$sum_i$在$A$左侧的时候,$w(k,i)$和$w(j,i)$都在下降,而$sum_i$离$x=-q$更远,$w(j,i)$下降更快(增长速度小)
- 当$sum_i$在$A,B$之间时,$w(k,i)$在上升,$w(j,i)$在下降
- 当$sum_i$在$B$右侧时,$w(k,i)$和$w(j,i)$都在上升,而$sum_i$离$x=-q$更近,$w(j,i)$增长更慢
综上,$w(k,i)$增长速度比$w(j,i)$快,满足决策单调性。
考虑如何优化。既然有决策单调性了,决策点与位置会有这样的关系:
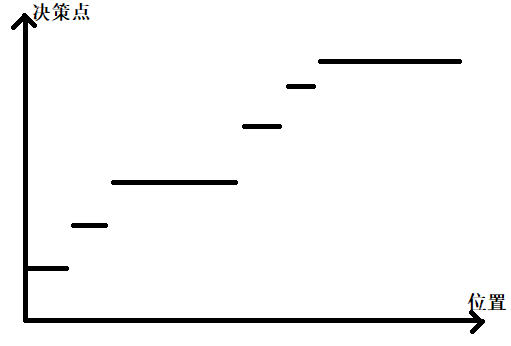
每个决策点控制了一段连续的区间。
于是可以维护一个决策点的单调队列,其中存有若干三元组$(p_i,l_i,r_i)$表示决策点$p_i$当前控制区间$[l_i,r_i]$的转移,队尾三元组一定满足$r_{tail}=n$。
转移时,弹出队头直到$i\in[l,r]$,然后直接转移。
之后我们得到了一个新的决策点$i$,分步进行:
- 判断$n$以$i$为决策点是否不如$p_{tail}$优,如果在位置$n$都干不过队尾的话就可以当场去世了。
- 否则,不断判断$l_{tail}$以$i$为决策点转移是否比$p_{tail}$更优。如果$i$在$l_{tail}$都比$p_{tail}$优的话,后面的位置就更不用说了,把队尾踢掉好了。
- 最后,显然控制区间是有单调性的。根据$[l_{tail},r_{tail}]$二分出左端点(右端点为$n$),更新队尾的$r_{tail}$并把$i$压入队尾。
复杂度$O(n\log n)$。
要判断答案是否超过$10^{18}$,直接long long的话会爆炸,用long double存储。
代码
long double f[maxn];
int sum[maxn],pos[maxn],ll[maxn],rr[maxn],w[maxn],l,p;
char s[maxn][31];
inline long double quickpow(long double x,int y){
long double ans=1.0;
while(y){
if(y&1)ans*=x;
x*=x,y>>=1;
}
return ans;
}
void print(int p){
if(!p)return;
print(pos[p]);
for(register int i=pos[p]+1;i<p;++i)printf("%s ",s[i]);
printf("%s\n",s[p]);
}
inline long double calc(int j,int i){return f[j]+quickpow(abs(sum[i]-sum[j]-l-1),p);}
inline int getpos(int l,int r,int p,int q){
while(l<r){
int mid=l+r>>1;
if(calc(p,mid)<calc(q,mid))r=mid;
else l=mid+1;
}
return l;
}
int main(){
int t=read();
while(t--){
int n=read(),h=1,t=0;
l=read(),p=read();
for(register int i=1;i<=n;++i)scanf("%s",s[i]),sum[i]=sum[i-1]+strlen(s[i])+1;
ll[++t]=1,rr[t]=n,w[t]=0;
for(register int i=1;i<=n;++i){
while(h<=t&&rr[h]<i)++h;
f[i]=calc(pos[i]=w[h],i);
if(calc(i,n)>=calc(w[t],n))continue;
while(h<=t&&calc(i,ll[t])<calc(w[t],ll[t]))--t;
rr[t]=getpos(ll[t],rr[t]+1,i,w[t])-1,++t,ll[t]=rr[t-1]+1,rr[t]=n,w[t]=i;
}
if(f[n]>1e18)puts("Too hard to arrange");
else {
printf("%lld\n",(long long)(f[n]+0.5));
print(n);
}
puts("--------------------");
}
}
利弊
二分的好处是能动态加入决策点,方程中未计算出的$f$不影响维护决策单调性(这一点在分治中能体现出来)。
而缺点是必须能快速计算$w(j,i)$。
分治
普通分治
其实算不上DP,只是用决策单调性优化而已
移个项:$a_j+\sqrt{|i-j|}-a_i\le p$
则$ans_i=\max\{a_j+\sqrt{|i-j|}\}-a_i$。
分类去掉绝对值:$ans_i=\max\{\max\limits_{j< i}\{a_j+\sqrt{i-j}\},\max\limits_{j>i}\{a_j+\sqrt{j-i}\}\}-a_i$
因为前一半翻转过来再求一遍就是后一半,所以只考虑$\max\limits_{j<i}\{a_j+\sqrt{i-j}\}$。
同样通过打表,可以发现满足决策单调性。
严格证明也好说,显然函数$f(x)=x^{\frac{1}{2}}$的增长速度是越来越慢的,就能证出来,不再赘述。
分治的基础是根据决策单调性,如果已知$i$的决策点$p_i$,则$\forall j< i,p_j\le p_i$;$\forall j>i,p_j\ge p_i$。
维护一个位置区间$[l,r]$和决策点区间$[L,R]$,表示$\forall i\in[l,r],p_i\in[L,R]$。初始都是$[1,n]$。
分治时,取$[l,r]$的中点$mid$,暴力遍历$[L,R]$得到$p_{mid}$,然后继续分治$([l,mid-1],[L,p_{mid}])$和$([mid+1,r],[p_{mid},R])$。
复杂度还是容易算的:一共递归$O(\log n)$层,每层遍历的$[L,R]$之和是$O(n)$的,总复杂度为$O(n\log n)$。
代码1
double f[maxn],ans[maxn];
int a[maxn];
void solve(int l,int r,int L,int R){
if(l>r)return;
int mid=l+r>>1,p;
for(register int i=min(mid,R);i>=L;--i)if(f[mid]<a[i]+sqrt(mid-i))f[mid]=a[i]+sqrt(mid-i),p=i;
solve(l,mid-1,L,p);
solve(mid+1,r,p,R);
}
int main(){
int n=read();
for(register int i=1;i<=n;++i)a[i]=read();
solve(1,n,1,n);
for(register int i=1;i<=n;++i)ans[i]=f[i],f[i]=0.0;
reverse(a+1,a+1+n);
solve(1,n,1,n);
for(register int i=1;i<=n;++i)ans[i]=max(ans[i],f[n-i+1]);
reverse(a+1,a+1+n);
for(register int i=1;i<=n;++i)printf("%d\n",(int)ceil(ans[i])-a[i]);
}
分治+莫队
本题中$w(j,i)$就是区间$[j,i]$的相同元素对数。
暴力很简单,设$f(i,j)$为前$j$个数分了$i$段的最小代价。
$f(i,j)=\min\limits_{k<j}\{f(i-1,k)+w(k+1,j)\}$
决策单调性的证明也很简单,把元素$a_{i+1}$分别添加到$[j,i]$和$[k,i]$($k<j$)中,一定有$\sum\limits_{x\in[j,i]}[a_x=a_{i+1}]<\sum\limits_{x\in[k,i]}[a_x=a_{i+1}]$,$w(j,i)$的增长速度比$w(k,i)$慢,满足决策单调性。
而现在最大的问题在于无法快速计算$w(j,i)$。
如果仅仅是多次询问$w(l,r)$且可以离线,第一想法肯定是莫队。
是不是可以把莫队的思想用到分治里呢?
维护两个指针,计算$w(j,i)$时就暴力把指针移动过去。但是分治就相当于强制在线了,不能对询问排序,只能按分治的顺序移动指针。
可以证明(懒),这样指针的移动次数是$O(n\log n)$的。
最终复杂度$O(nk\log n)$。
代码2
long long f[2][maxn],ans;
int tax[maxn],a[maxn],pl,pr;
inline void add(int x){ans+=tax[x],++tax[x];}
inline void del(int x){--tax[x],ans-=tax[x];}
inline void move(int j,int i){
while(pl<j)del(a[pl++]);
while(pl>j)add(a[--pl]);
while(pr>i)del(a[pr--]);
while(pr<i)add(a[++pr]);
}
void solve(int l,int r,int L,int R,bool o){
if(l>r)return;
int mid=l+r>>1,p;
for(register int i=min(mid-1,R);i>=L;--i){
move(i+1,mid);
if(f[o^1][i]+ans<f[o][mid])f[o][mid]=f[o^1][i]+ans,p=i;
}
solve(l,mid-1,L,p,o);
solve(mid+1,r,p,R,o);
}
int main(){
int n=read(),k=read();
for(register int i=1;i<=n;++i)a[i]=read();
memset(f[0],0x3f,sizeof f[0]),f[0][0]=0;
for(register int i=1;i<=k;++i){
memset(tax,0,sizeof tax),ans=0,pl=1,pr=0;
memset(f[i&1],0x3f,sizeof f[i&1]);
solve(i,n,0,n,i&1);
}
printf("%lld\n",f[k&1][n]);
}
利弊
最大的优点就是通过莫队的思想可以解决一些$w(j,i)$无法快速计算的问题。再一个分治更好理解,代码好写。
所以请读者尝试写一下「诗人小G」的分治做法。

是不是发现问题了?
在「诗人小G」中,$f$数组是由自身转移过来的。而在后两道题中,$f$是由无关的数组转移的。
而分治的过程中取了$[l,r]$中点计算,没有按顺序转移。其局限性就在于不能处理自身的转移。
水题
注:毕竟这是篇决策单调性学习笔记,下面的题肯定都满足决策单调性。。。而实际应用中这玩意还是要想到并且打表证明出来的。所以所有题均不予证明决策单调性,留给读者自证。
邮局
$w(j,i)$为在村儿$[j,i]$中建一个邮局最小的距离和。
显然建在中点是最优的。维护个坐标前缀和就可以$O(1)$算了。
设$f(i,j)$为在前$j$个村儿里造$i$个邮局的最小代价。
枚举第$i$个邮局的控制范围转移:$f(i,j)=\min\limits_{k<j}\{f(i-1,k)+w(k+1,j)\}$
看起来这个方程有点别扭,可能$[k+1,j]$里有的村儿最近的邮局不是$i$啊。但这样的话这个转移一定不优,会有一个更大的$k$让这些村儿往最近的邮局跑。
任务分配问题
简单地说就是把序列分成$k$段,段内顺序对之和最小。
设$f(i,j)$为前$j$个数分了$i$段的最小顺序对,$w(j,i)$为区间$[j,i]$的顺序对数。
$f(i,j)=\min\limits_{k<j}\{f(i-1,k)+w(k+1,j)\}$
分治+莫队套个树状数组即可,$O(nk\log^2n)$的。
柠檬
决策单调性请右转题解区吧,因为我写的斜率优化。。。







