感jo长链剖分要写的东西不是很多（其实也不少），但感觉很$dio$干脆新开一篇了（

前言

和重链剖分一样，长链剖分也是把树划分成若干条链的方式。

重链剖分是以子树大小划分的，而长链剖分是以点的深度划分的。

抄袭来源

https://www.cnblogs.com/cjyyb/p/9479258.html

https://blog.csdn.net/litble/article/details/87965999

#define

$son(x)$：$x$的长儿子。

$md(x)$：$x$与其子树内最远点的距离。

$top(x)$：长链链顶。

$seg(x)$：$x$的$dfs$序。

长链剖分

实现

以$md$最大的儿子为自己的长儿子，剩下的和重链剖分完全一样。

代码

int md[maxn],son[maxn],top[maxn],h[maxn];
bool vis[maxn];
struct edge{int h[from],to;}e[maxn<<1];
void dfs1(int node){
    md[node]=1;
    for(register int i=h[node],x;i;i=e[i].pre){
        x=e[i].to;
        if(md[x])continue;
        dfs1(x);
        if(md[x]>md[son[node]])son[node]=x,md[node]=md[x]+1;
    }
}
void dfs2(int node){
    vis[node]=1;
    if(!son[node])return;
    top[son[node]]=top[node],dfs2(son[node]);
    for(register int i=h[node],x;i;i=e[i].pre){
        x=e[i].to;
        if(!vis[x])top[x]=x,dfs2(x);
    }
}

性质

1.所有长链链顶的$md$之和是$O(n)$的。

长链一定是延伸到叶节点的，也就是说长链的长度等于链顶的$md$。

而长链互不相交，且每个点只属于一条长链。所以长链长度之和是$O(n)$的。

2.从一个点向上跳top，长链的长度单调递增。

考虑反证法。

若长链的长度变短了：

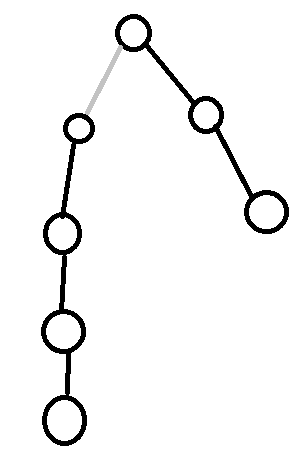
非常直观了吧，此时一个更深的儿子反而不是长儿子，不符合定义。

3.从一个点向上跳top，最多跳$\sqrt n$次到达根节点。

根据性质$2$，最坏情况下到达的长链长度为$1,2,3\dots\sqrt n$，使它们和为$n$。

不过毕竟是$\sqrt n$，长剖求$lca$并不优秀。

4.任意一个点的$k$级祖先所在的长链长度不低于$k$。

都已经是$k$级祖先了，所以至少存在一条链长度为$k$。

应用

dsu on tree·改

一般所说的$dsu\ on\ tree$是基于重链剖分的：

访问轻儿子，回溯时清空信息
访问重儿子，保留信息
暴力把轻儿子的信息统计上，得到当前节点子树信息

当然这里不是用长剖来$dsu$，复杂度成$O(n\sqrt n)$了。

注意保留重儿子信息这一点，用到长剖上会怎么样？

实现

例题

设$f(i,j)$为以点$i$为根的子树中，与$i$距离为$j$的点的数量。这个题实际上就是求最大的$f(i,j)$中的$j$。

转移很简单：$f(i,0)=1,f(i,j)=\sum\limits_{fa(x)=i}f(x,j-1)$

这样是$O(n^2)$的。

考虑保留长儿子的信息，我们发现$f(i)$其实就是$f(son(i))$平移了一位，通过指针可以$O(1)$继承长儿子的信息（具体实现见代码）。

而短儿子~~（听起来好像很别扭）~~直接暴力转移即可。

代码

int h[maxn],md[maxn],son[maxn],tax[maxn<<1],ans[maxn],*f[maxn],*p=tax,num;
struct edge{int pre,to;}e[maxn<<1];
inline void add(int from,int to){e[++num]=(edge){h[from],to},h[from]=num;}
void dfs(int node=1){
    md[node]=1;
    for(register int i=h[node],x;i;i=e[i].pre){
        x=e[i].to;
        if(md[x])continue;
        dfs(x);
        if(md[x]>md[son[node]])son[node]=x,md[node]=md[x]+1;
    }
}
void dp(int node=1,int fa=0){
    if(son[fa]!=node)f[node]=p,p+=md[node]<<1;//轻儿子申请数组空间
    if(son[node]){
        f[son[node]]=f[node]+1,dp(son[node],node);//直接使用重儿子的数组，继承重儿子的f
        if(ans[son[node]])ans[node]=ans[son[node]]+1;
    }
    f[node][0]=1;
    for(register int i=h[node],x;i;i=e[i].pre){
        x=e[i].to;
        if(x==fa||x==son[node])continue;
        dp(x,node);
        for(register int j=1;j<=md[x];++j){
            f[node][j]+=f[x][j-1];
            if(f[node][j]>f[node][ans[node]]||(f[node][j]==f[node][ans[node]]&&ans[node]>j))ans[node]=j;
        }
    }
}

也可以通过给节点编号继承，在用线段树维护$DP$的时候更方便。

复杂度

时间复杂度是$O(\sum\limits_{son(fa(i))\neq i}md(i))$的。

显然一个短儿子是它所在长链的链顶，那么根据性质$1$，$md$之和是$O(n)$的。所以时间复杂度是$O(n)$的。

而空间复杂度不高于时间复杂度，从代码也能看出来和时间复杂度同级。

对于这种和复杂度和深度有关的，可以考虑长剖优化。

求k级祖先

实现

在此之前，求$k$级祖先可以倍增$O(n\log n)-O(\log n)$、树剖$O(n)-O(\log n)$和离线$dfs$+栈$O(n)$。

而用长剖可以做到在线$O(n\log n)-O(1)$。

板子

首先在每条长链的链顶存下链中所有点和链顶的前$md$级祖先，根据性质$1$这是$O(n)$的。

查询$x$的$k$级祖先，要选择一个$r$，跳到$x$的$r$级祖先$y$，满足$r\le k\le 2r$。

根据性质$4$，此时的链顶一定存有$y$的$k-r$级祖先，要么在链顶的祖先里，要么在长链里。而前面已经存过了，$O(1)$获取即可。

选择$k$二进制下最高位的$1$作为$r$，然后倍增预处理出$x$的$2^r$祖先就行了。

代码

vector<int>u[maxn],d[maxn];
int md[maxn],son[maxn],top[maxn],fa[maxn][22],lg[maxn],h[maxn],deep[maxn],num;
struct edge{int pre,to;}e[maxn];
inline void add(int from,int to){e[++num]=(edge){h[from],to},h[from]=num;}
void dfs1(int node){
    md[node]=1;
    for(register int i=1;i<=lg[deep[node]];++i)
        fa[node][i]=fa[fa[node][i-1]][i-1];
    for(register int i=h[node],x;i;i=e[i].pre){
        x=e[i].to,fa[x][0]=node,deep[x]=deep[node]+1,dfs1(x);
        if(md[x]>md[son[node]])son[node]=x,md[node]=md[x]+1;
    }
}
void dfs2(int node){
    d[top[node]].push_back(node);
    if(top[node]==node)for(register int i=1,x=fa[node][0];i<=md[node]&&x;x=fa[x][0],++i)u[node].push_back(x);
    if(!son[node])return;
    top[son[node]]=top[node],dfs2(son[node]);
    for(register int i=h[node],x;i;i=e[i].pre){
        x=e[i].to;
        if(x!=son[node])top[x]=x,dfs2(x);
    }
}
int query(int x,int k){
    if(!k)return x;
    x=fa[x][lg[k]],k^=1<<lg[k];
    if(k<=deep[x]-deep[top[x]])return d[top[x]][deep[x]-deep[top[x]]-k];
    return u[top[x]][k-deep[x]+deep[top[x]]-1];
}
#define ui unsigned int
ui s;
inline ui get(ui x) {
    x ^= x << 13;
    x ^= x >> 17;
    x ^= x << 5;
    return s = x; 
}
int main(){
    int n=read(),m=read(),root,ans=0;
    long long res=0;
    s=read<unsigned int>();
    for(register int i=2;i<=n;++i)lg[i]=lg[i>>1]+1;
    for(register int i=1,x;i<=n;++i){
        x=read();
        if(!x)root=i;
        else add(x,i);
    }
    deep[root]=1,top[root]=root,dfs1(root),dfs2(root);
    for(register int i=1;i<=m;++i){
        int x=(get(s)^ans)%n+1,k=(get(s)^ans)%deep[x];
        ans=query(x,k),res^=1ll*ans*i;
    }
    printf("%lld\n",res);
}

水题

HOT-Hotels

洛谷上也有，不过是弱化版。

~~难点其实是DP。~~

距离两两相等的三个点会长成这样：

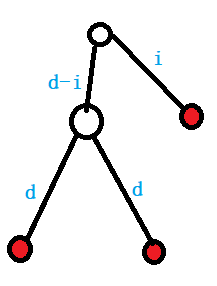
设$f(i,j)$为以点$i$为根的子树中，与$i$距离为$j$的点的数量；$g(i,j)$为以点$i$为根的子树中，点对$(x,y)$的数量，满足$dis(lca(x,y),x)=dis(lca(x,y),y)=dis(lca(x,y),i)+j$。

转移和统计答案显然：

$f(i,0)=1,f(i,j)=\sum\limits_{fa(x)=i}f(x,j-1)$
$g(i,0)=\sum\limits_{fa(x)=i}g(x,1),g(i,j)=\sum\limits_{fa(x)=i}g(x,j+1)+f(i,j)\times f(x,j-1)$
$ans+=g(i,0)+\sum\limits_{fa(x)=i}g(i,j)\times f(x,j-1)+g(x,j+1)\times f(i,j)$

长剖优化即可。

重建计划

以前用点分治写过，以下都是口胡。

见平均值想$01$分数规划，二分走起。

然后就是找一条长度在$[L,R]$之间、权值和最大的路径。

~~点分治+单调队列啊~~

设$f(i,j)$为以点$i$为根的子树中，点$i$为一端长度为$j$的路径最大值。

$f(i,j)=\max\limits_{fa(x)=i}\{f(x,j-1)\}$

$ans=\max\limits_{k\in[L,R]}\{f(i,k)\}$

区间求$\max$需要套个线段树，指针就不管用了，要用编号来处理。

长剖的时候求一下$dfs$序。和树剖一样先遍历长儿子。

维护一颗蛇皮的全局线段树，位置$seg(i)+j$表示$f(i,j)$。这样就可以直接继承了。

攻略

题解

希望

告辞.jpg

长链剖分学习笔记

前言