学一个算法,就要把它学精了,理解透彻了。——某金牌教练
所以我要多快好省、不求甚解地大量学习算法。
前言
本来想挺进多项式,因为要耗费太多精力先放放。
感觉我会的东西好少啊,学弟们会的算法都比我多。
于是来清一波任务清单。很多算法都太小了就把学习笔记合到一块了。
抄袭来源
https://www.luogu.com.cn/blog/user9012/ke-lu-si-ka-er-zhong-gou-shu-lve-xie
https://www.luogu.com.cn/problemnew/solution/P3805
https://www.luogu.com.cn/problemnew/solution/P2365
https://www.cnblogs.com/twilight-sx/p/9064208.html
https://blog.csdn.net/Adolphrocs/article/details/88756533
https://blog.csdn.net/a_forever_dream/article/details/83654397
https://ouuan.github.io/%E7%BA%BF%E6%80%A7%E5%9F%BA%E5%AD%A6%E4%B9%A0%E7%AC%94%E8%AE%B0/
https://www.cnblogs.com/cjjsb/p/9771868.html
kruskal重构树
构造
在kruskal的过程中合并两个联通块时,新建一个节点作为重构树上这两个联通块的根的父亲,把该节点的点权设为当前边边权就行了。
也就是把fa[u]=v改成a[++cnt]=e[i].l,fa[u]=cnt,fa[v]=cnt。
性质
以最小生成树为例。
1.kruskal重构树是一棵二叉树
2.原图中的点在重构树上都是叶子节点
3.点权随深度增加而递减
4.定义一条路径的权值是其最大边权。原图上两点之间所有路径的最小权值,等于重构树上两点$lca$的点权
应用
一个无向连通图,多次询问,给定一个点,只走边权不超过$k$的边,求出所有能到达的点中#@%^&。
在重构树上倍增到第一个权值小于等于$k$的点,它的子树就是能到达的点。
因为根据性质2,3,如果再往上走的话,经过的边权就大于$k$了。
选取合适的数据结构维护子树信息即可。
水题
Peaks
求子树第$k$大直接$dfs$序+主席树就好了。
归程
跑一遍点$1$的最短路,以最短路距离作为点权,答案就是子树$\min$。
werewolf狼人
题意就是一张无向连通图上,给定两个点$s,e$,询问是否存在一个点$x$,使得$s$到$x$的路径上点的编号都大于等于$L$,且$x$到$e$的路径上点的编号都小于等于$R$。
分别对最小生成树和最大生成树造kruskal重构树。走一条边一定是两端点都经过了,所以边权分别为$\max(x,y)$和$\min(x,y)$。
让$s$和$e$分别在最小重构树和最大重构树上倍增到合适节点,判断两个子树是否有交,主席树或离线树状数组皆可。
manacher
莫名其妙两点睡的困死了大脑已停止工作看不懂矩阵树嘤嘤嘤先学马拉车了
#define
$ma(i)$:以字符$i$为对称轴,向两边扩展的最长回文半径。也就是说开区间$(i-ma(i),i+ma(i))$为回文串。
$R$:当前所有回文子串能扩展到的最靠右的端点。
$mid$:$R$对应的对称轴。
实现
回文子串的对称轴可能是一个字符,也可能是字符间隙。
在$S$的开头、结尾和字符之间插入特殊字符#,两种情况就可以一块处理了。为了便于处理越界情况,在最开头再插一个#。
举个栗子:manacher $\rightarrow$ ##m#a#n#a#c#h#e#r#
扫一遍串,对于当前位置$i$:
- 若$i\le r$,取$i$关于$mid$的对称点$j$(易知$j=mid\times 2 -i$)。$i,j$在同一回文子串中对称,所以有$ma(i)=ma(j)$。但因为该回文串右端点是$R$,$i+ma(j)$不能超过$R$,所以要对$R-i+1$取$\min$。
- 若$i>r$,直接从$1$开始暴力向两边拓展得到$ma(i)$。
最后更新$R$和$mid$。
答案为$\max\{ma(i)\}-1$。
板子
int ma[maxn<<1];
char a[maxn],s[maxn<<1],n,len;//a为给定串,n为其长度。s为插入特殊字符后的串,len为其长度
void manacher(){
s[0]='$';
for(register int i=1;i<=n;++i)s[++len]='$',s[++len]=a[i];
s[++len]='$';
int ans=0,R=0,mid;
for(register int i=1;i<=len;++i){
if(i<=r)ma[i]=min(ma[(mid<<1)-i],r-i+1);
while(s[i-ma[i]]==s[i+ma[i]])++ma[i];
if(i+ma[i]-1>R)R=i+ma[i]-1,mid=i;
ans=max(ans,ma[i]);
}
printf("%d\n",ans-1);
}
终于不会出现用$hash$求回文串被卡只能默写后缀数组的情况了。
复杂度
时间复杂度为$O(|S|)$。
对于上面第一种情况,因为$ma$的定义是最大回文半径了,所以$i$继承的$ma$要么已经是最大的了,不需要拓展,复杂度为$O(1)$;要么右端点在$R$上,需要暴力拓展。
对于第二种情况,因为$i>R$,所以拓展出的右端点一定大于$R$。
因此只要暴力拓展,$R$一定会被更新。而$R$是单调不降的,故暴力拓展复杂度为$O(|S|)$。
斜率优化DP
实现
例题1
首先可以得到一个朴素的$DP$:
设$f(i)$为完成前$i$项任务最小代价,$t_i$为时间前缀和,$sum_i$为费用前缀和。因为启动时间$s$会对后面的人物都产生影响,$DP$时要算上对后面的贡献。
有转移$f(i)=\min\limits_{j<i}\{f(j)+t_i(sum_i-sum_j)+s(sum_n-sum_j)\}$
把这个式子变个形:
$f(j)=(t_i+s)sum_j+f(i)-t_isum_i-sum_ns$
后面那一坨$-t_isum_i-sum_ns$是个常数,先不要管它。
如果把这个式子看作直线方程的话,那它就表示斜率为$t_i+s$,截距为$f(i)$,过点$(sum_j,f(j))$的直线,而我们的目的是最小化截距$f(i)$。
有一条已知斜率的直线和若干点,找一个点使该直线与$y$轴交点尽量靠下。就是把直线往上面移动,碰到的第一个点就是转移点。
考虑什么样的点会使转移点:
先把点按横坐标排序,相邻点连线。首先能排除掉像这样的上凸包顶点:
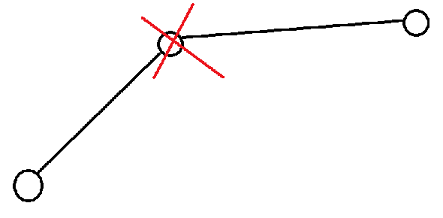
那么剩下的点连出来的直线斜率是递增的,大概可以$yy$出来转移点是长这样的:
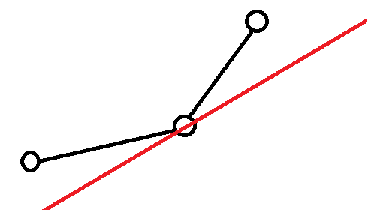
也就是给定直线的斜率大于该点前一条直线的斜率、小于该点后一条直线的斜率。
于是我们要做的是:
- 维护相邻点连线斜率递增的若干个点
- 查询给定斜率的后继
就本题而言,横坐标$sum$是递增的,可以用单调队列维护第一条,不断弹出队尾直到队尾和前一个点的斜率小于给定点和队尾的斜率。
而$sum+t$也是递增的,查询时直接弹出队首直到队首和第二个点的斜率大于给定斜率,这时队首就是转移点。
代码1
用乘法代替直接计算斜率,避免浮点数误差,还能优化常数。
int sum[maxn],t[maxn],f[maxn];
struct Monoqueue{
int x[maxn],y[maxn],p[maxn],head,tail;
void push(int xx,int yy,int pos){
while(head<tail&&1ll*(xx-x[tail])*(y[tail]-y[tail-1])>=1ll*(x[tail]-x[tail-1])*(yy-y[tail]))--tail;
x[++tail]=xx,y[tail]=yy,p[tail]=pos;
}
void check(int k){while(head<tail&&y[head+1]-y[head]<k*(x[head+1]-x[head]))++head;}
int front(){return p[head];}
Monoqueue(){head=1,tail=0;}
}q;
int main(){
int n=read(),s=read();
for(register int i=1;i<=n;++i)t[i]=t[i-1]+read(),sum[i]=sum[i-1]+read();
q.push(0,0,0);
for(register int i=1;i<=n;++i){
q.check(t[i]+s);
int j=q.front();
f[i]=f[j]+t[i]*(sum[i]-sum[j])+s*(sum[n]-sum[j]);
q.push(sum[i],f[i],i);
}
printf("%d\n",f[n]);
}
例题2
和例题1不同的是时间有负数。
也就是说斜率不单调了,不能通过弹出队首找后继了。但因为队里的元素都是递增的,直接二分即可。
同理,如果横坐标不递增,就要用平衡树或cdq分治维护了。
代码2
其他地方都差不多就只放二分的代码了:
inline int find(long long k){
int l=1,r=tail,mid;
while(l<r){
mid=l+r+1>>1;
if(y[mid]-y[mid-1]<=k*(x[mid]-x[mid-1]))l=mid;
else r=mid-1;
}
return p[l];
}
水题
剽的一本通的题。。。然而都是套路。。。
玩具装箱TOY
设$f(i)$为前$i$件物品的最小费用,$sum_i$为$C_i$的前缀和。容易得到$f(i)=\min\{f(j)+(i-j-1+sum_i-sum_j-L)^2\}$。
令$s_i=i+sum_i,t_i=i+sum_i-L-1$,方程经过变形可以得到:
$f(j)+s_j^2=f(i)+2t_is_j-t_i^2$
$2t_i$为斜率,$s_j$为横坐标,且这两者递增。$f(j)+s_j^2$为纵坐标,单调队列维护即可。
Cats Transport
对$d$做个前缀和,令$s_i=t_i-d_{h_i}$,即从$s_i$时刻出发恰好能接上猫$i$。
对$s_i$排个序,令$sum_i$为其前缀和。
设$f(i,j)$为接了按$s$排好序的前$i$只猫,已经用了$j$个铲屎官的最小等待时间。
枚举先接哪只猫,转移:$f(i,j)=\min\limits_{k\le i}\{f(k,j-1)+s_i(i-k)-sum_i+sum_k\}$
变形得$f(k,j-1)+sum_k=f(i,j)+s_ik-is_i+sum_i$
以$s_i$为斜率,$k$为横坐标,$f(k,j-1)+sum_k$为纵坐标,用单调队列维护斜率优化。
仓库建设
令$t_i=\sum\limits_{j=1}^ip_j,s_i=\sum\limits_{j=1}^ip_jx_j$。
设$f(i)$为前$i$个工厂都$OK$的最小费用。
$f(i)=\min\limits_{j<i}\{f(j)+(t_i-t_j)x_i-s_i+s_j\}+c_i$
剩下的套路不用说了吧。
特别行动队
本来期待$APIO$的题能有什么东西的,结果还是没意思。。。
令$s_i=\sum\limits_{j=1}^ix_j$
$f(i)=\max\limits_{j<i}\{f(j)+a(s_i-s_j)^2+b(s_i-s_j)+c\}$
唯一不同的是取$\max$正好反过来,要维护一个斜率递减的点集。
锯木厂选址
令$D_i=\sum\limits_{j<i}d_i,t_i=\sum\limits_{j\le i}w_j,s_i=\sum\limits_{j\le i}w_jD_j$
设$g(i)$为前$i$棵树,只有$i$有一个锯木厂的花费,$f(i)$为前$i$棵树已经有两个锯木厂,且$i$有一个锯木厂的最小花费。
$g(i)=D_it_i-s_i$
$f(i)=\min\limits_{j<i}\{g(j)+D_i(t_i-t_j)-s_i+s_j\}$
最后答案在$f(i)+D_{n+1}(t_n-t_i)-s_n+s_i$里取$\min$。
序列分割
矩阵树定理
内容
详情请咨询组合数学食用笔记
水题
小Z的房间
板子题。唯一要注意的是柱子不能放进Kirchhoff矩阵中。
黑暗前的幻想乡
枚举集合$S$表示哪些公司没有修路容斥。对剩下的公司矩阵树定理求方案数。
即$ans=\sum\limits_{S}(-1)^{|S|}calc(S)$
复杂度$O((n-1)^32^{n-1})$
重建
最小生成树计数
线性基
定义
对一个数的集合$S$,其线性基就是由最少的数(最小性)构成的集合$B$,满足从$S$中任取一些数异或起来(不包括$0$)得到的值域,与$B$中任取一些数异或起来得到的值域相同。
性质
1.对于任意的$i$,$B$中最多只有一个元素二进制下最高位的$1$为第$i$位(下记该元素为$B_i$)
2.取$B$中任意元素异或起来结果不为$0$
3.对于任意$B$的元素$x$,不存在取$B$中若干其他元素异或起来等于$x$
4.若$S$的值域上界为$2^n-1$,则$B$最多有$n$个数
构造
插入
考虑插入元素$x$的影响:根据性质$3$,如果当前线性基能异或出$x$,就不管$x$;否则添加某个数使线性基能异或出$x$。
怎么得到$x$呢?根据性质$1$,异或$B_i$(如果$B_i$有值)对$i$以上的位没有影响。从高到低考虑,如果$x$第$i$位上为$1$,就让$x$异或上$B_i$。如果$B_i$不存在就$gg$了,这时我们需要把$x$放到$B_i$上。
插入复杂度$O(\log V)$,$V$为值域。
插入代码:
long long b[61];
void insert(long long x){
for(register int i=60;~i;--i){
if(x>>i&1){
if(!b[i]){b[i]=x;return;}
x^=b[i];
}
}
}
合并
把$S_1$和$S_2$的线性基合并,得到的新线性基对应的集合$S=S_1\cup S_2$。
显然直接把$S_1$插到$S_2$里就行,复杂度$O(\log^2V)$。
应用
判断是否能从S中取若干数异或得到x
把$x$插入线性基看看是否插入成功就行了。
子集异或最大值
从高到低贪心,若当前答案第$i$位本来就有$1$,不用管;否则判断与$B_i$是否能异或出第$i$位的$1$(其实就是看看$B_i$是否存在),能就异或上$B_i$。
当然不用写这么麻烦,直接if((ans^b[i])>ans)ans^=b[i];就行。
子集异或最小值
就是$B$的最小值。
子集异或第k小
说实话还没有完全明白。。。
首先要魔改(其实是正规化)构造方式:
重新定义$B_i$为满足原来条件的最小值。
还是考虑插入$x$的影响,若$x$在第$i$位上$gg$了:
- 对于低位,$x$可以通过异或它们变得更小,从而使$B_i$最小
- 对于高位,它们异或$x$可能会变得更小
因此扫一遍更新即可。
代码:
void insert(long long x){
for(register int i=60;~i;--i){
if(x>>i&1){
if(!b[i]){
for(register int j=i-1;~j;--j)if(x>>j&1)x^=b[j];
for(register int j=i+1;j<=60;++j)if((b[j]^x)<b[j])b[j]^=x;
b[i]=x;
return;
}
x^=b[i];
}
}
}
然后把有值的$B_i$提出来排好,得到的数组记为$A$。把$k$二进制拆分,答案就是为$1$的位的$A$的异或和。
由于不能选空集,会有一些细节自己研究去吧我就懒得说了
水题
元素
按魔法值从大到小排序,依次插入线性基,如果成功插入就选。
彩灯
翻译一下,若干个$n$位二进制数,取任意个异或起来有多少种不同的结果?
因为这和在线性基取若干数是等价的,若线性基有$cnt$个数,还可以取空集,答案就是$2^{cnt}$。
幸运数字
基于线性基的合并用数据结构维护线性基。
可以倍增,也可以点分治,题解区五花八门的。
记$M(A,B)$为$A,B$合并得到的新线性基,显然有性质$M(M(A,B),C)=M(M(A,B),M(B,C))$。
也就是说合并有重叠性,可以$ST$表维护。于是我选择了树剖+$ST$表,$3$个$\log$。不过合并一般跑不满所以能过。
最大XOR和路径
题解第一篇讲的很清楚了。
装备购买
第一道水题的实数版。
OI中的线性基一般都是指上面的异或线性基,这道题就是实数的线性基了。
考虑把异或拓展到实数运算上:
构造异或线性基的时候,其实是把每个数看作$n$维向量,对每一维考虑,若为$1$就异或上$B_i$来消掉这一位的$1$,不存在$B_i$就赋值为该数。
同理,对于实数线性基,把一组数也看作$n$维向量,对有值的位,若$B_i$存在,就消掉该位;否则赋值$B_i$为该实数集。
怎么消啊?类似于高斯消元搞一搞就行了。
2-SAT
都9102年了我还在学图论基础算法
定义
有一堆变量$a$,现在要给它们赋值为$0$或$1$。
$k-SAT$问题就是有若干条限制$b$,每条形如$(a_{b_1}=0/1)\lor (a_{b_2}=0/1)\lor \dots \lor (a_{b_k}=0/1)$,问是否存在一种赋值方案满足这些限制。
$k-SAT$是$NP$完全问题,但当$k=2$时可做。
复读一遍$2-SAT$的定义:$2-SAT$即有若干条限制$b$,每条形如$(a_{b_1}=0/1)\lor (a_{b_2}=0/1)$,问是否存在一种赋值方案满足这些限制。
判定
把$a_i$拆成两个点$a_{i,0}$和$a_{i,1}$,分别表示$a_i=0/1$。
用有向边$a_{i,x}\rightarrow a_{j,y}$表示$a_i=x\Rightarrow a_j=y$。
对于一条限制,比如是$a_3=0\lor a_4=0$,就要将$a_{3,1}$向$a_{4,0}$连边,$a_{4,1}$向$a_{3,0}$连边。
当从$a_{i,0}$沿着边走能走到$a_{i,1}$,且$a_{i,1}$能走到$a_{i,0}$,即$a_i=0\Leftrightarrow a_i=1$,矛盾,就不存在合法方案。
于是大力缩点判断$a_{i,0}$与$a_{i,1}$是否在同一强连通分量里即可解决。
输出方案
枚举每个变量赋值为几。
为了造成尽可能少的影响,直接选$a_{i,0}$和$a_{i,1}$中拓扑序较大的;或者说我们的目的是选拓扑序较大的一些点,就能保证构造出合法方案。
而$Tarjan$缩完点给强连通分量的编号就是逆序拓扑序,所以不用再拓扑排序了。
如果要求按字典序输出,没啥好方法,枚举每个变量选哪个判定是否可行,复杂度$O(nm)$。
代码
#define px(x) putchar(x)
#define ps px(' ')
#define pn px('\n')
struct edge{int pre,to;}e[maxn<<1];
int h[maxn],seg[maxn],low[maxn],sta[maxn],id[maxn],cnt,num,all,top;
bool vis[maxn];
inline void add(int from,int to){e[++num]=(edge){h[from],to},h[from]=num;}
void TJ(int node){
vis[sta[++top]=node]=1;
seg[node]=low[node]=++cnt;
for(register int i=h[node],x;i;i=e[i].pre){
x=e[i].to;
if(!seg[x])TJ(x),low[node]=min(low[node],low[x]);
else if(vis[x])low[node]=min(low[node],seg[x]);
}
if(seg[node]==low[node]){
id[node]=++all,vis[node]=0;
while(sta[top]!=node)id[sta[top]]=all,vis[sta[top--]]=0;
--top;
}
}
int main(){
int n=read(),m=read();
while(m--){
int a=read(),x=read(),b=read(),y=read();
add(a+(x^1)*n,b+y*n),add(b+(y^1)*n,a+x*n);
}
for(register int i=1;i<=n<<1;++i)if(!seg[i])TJ(i);
for(register int i=1;i<=n;++i)if(id[i]==id[i+n]){puts("IMPOSSIBLE");return 0;}
puts("POSSIBLE");
for(register int i=1;i<=n;++i)px(48+(id[i+n]<id[i])),ps;
pn;
}
水题
Flags
最小距离最大显然要二分。
二分判定显然是$2-SAT$。记$a_{i,0/1}$分别为$x_i$和$y_i$。如果存在$a_{i,x}-a_{j,y}<mid$且$a_{i,x}\ge a_{j,y}$,则两者不能同时选,连边$a_{i,x}\rightarrow a_{j,y\ xor\ 1},a_{j,y}\rightarrow a_{i,x\ xor 1}$。
复杂度爆炸显然要线段树优化建图。
有个坑点是直接连区间会把$a_{i,0}$和$a_{i,1}$连出来环,要把区间里的$a_{i,0}$抠出来。显然不好写。
游戏
如果没有x就是裸的$2-SAT$。对于限制$(i,x,j,y)$,连边$a_{i,x}\rightarrow a_{j,y},a_{j,y\ xor\ 1}\rightarrow a_{i,x\ xor\ 1}$。
$3^d$爆搜每个x的状态时间爆炸。发现x为a,b的时候已经把c的情况包含进去了,$2^d$爆搜即可。
Radio Stations
差分约束
都9102年了我还在学图论基础算法(复读)
而且后天就0202年了
板子
有$n$个变量$a_{1\dots n}$,$m$个限制形如$a_i-a_j\le c$。
这个长得很像最短路里的三角形不等式:$a_i-a_j\le c\rightarrow a_j+c\ge a_i\rightarrow dis_j+c\ge dis_i$。
把$j$向$i$连一条权值为$c$的边,建一个超级源向每个点连一条$0$边。跑一遍最短路,存在负环就无解。
方案就是$a_i=dis_i$。
板子代码
只判断可行性,直接广搜$spfa$会$T$,需要$dfs$版$spfa$。
struct edge{int pre,to,l;}e[maxn<<1];
int dis[maxn],cnt[maxn],h[maxn],num;
bool vis[maxn];
queue<int>q;
inline void add(int from,int to,int l){e[++num]=(edge){h[from],to,l},h[from]=num;}
void dfs(int node){
vis[node]=1;
for(register int i=h[node],x;i;i=e[i].pre){
x=e[i].to;
if(dis[x]>dis[node]+e[i].l){
if(vis[x]){puts("No");exit(0);}
dis[x]=dis[node]+e[i].l,dfs(x);
}
}
vis[node]=0;
}
int main(){
int n=read(),m=read();
for(register int i=1;i<=n;++i)add(0,i,0);
while(m--){
int s=read(),a=read(),b=read();
if(s==1)add(b,a,read());
else if(s==2)add(a,b,-read());
else add(b,a,0);
}
memset(dis,0x3f,sizeof dis),dis[0]=0;
dfs(0);
puts("Yes");
}
水题
糖果
本来是并查集+拓扑排序水题的,不过差分约束也能骗分搞。
连边关系显然,不过为了计算糖果数要按最长路的连。因为每个人都要有糖果,源点向每个点连的边权为$1$。
答案就是$dis$之和。
然后这个题卡$spfa$,第$5$个点要双端队列优化,第$6$个测试点源点向$1\sim n$要逆序连边。
倍杀测量者
任意情况都有人女装$\rightarrow$所有人都不女装不合法。
显然可以二分答案。
对两种条件,分别用$a_i\ge (k-T)a_j$和$a_i\ge \frac{1}{k+T}a_j$表示。
对已经确定的人,用$a_i\ge 1\times x$且$1\times x\ge a_i$表示。
取对数跑最长路,有正环就可以。
布局
很容易转成最短路来做,先判一下负环。
如果合法,假设答案为$ans$,显然$ans$为满足$dis_n-dis_1\ge ans$的最大值。实际上这就是从$n$到$1$连了一条长为$-ans$的边,且不会产生负环。
以$1$为起点跑一遍最短路,$dis_n$即为答案。
莫队
其实我是会莫队的,不过还没有系统地学过莫队全家桶,在这写一写。
树上莫队
搞出来树的括号序:$dfs$整棵树。对于点$i$,进入时加入$i$记为$st_i$,回溯时再加进去记为$en_i$。
然后把询问$(x,y)$分两种情况扔到括号序上:
- $lca(x,y)=x$:$[st_x,st_y]$($lca(x,y)=y$一样)
- $\operatorname{otherwise}$:$[en_x,st_y]$(假设$en_x<st_y$)此时$lca$没有算上,要额外计算。
在括号序上跑莫队。出现过奇数次的点算上贡献,偶数次不算。
带修莫队
按左端点的块为第一关键字、右端点的块为第二关键字、时间为第三关键字排序,块大小设置为$n^{\frac{2}{3}}$,维护左右端点和时间三个指针即可,复杂度$O(n^{\frac{5}{3}})$。
回滚莫队
如果莫队的添加容易,删除麻烦(或者反过来),可以考虑回滚莫队。
排序还是一样的。把左端点都在同一个块(假设块的区间为$[L,R]$)里的一块处理,维护一个右指针$pr$,初始值为$R$。对于询问$[l,r]$:
- 若$l$与$r$在同一个块里,暴力。
- 否则,移动$pr$到$r$,加上$[pr+1,r]$的贡献(因为同一个块里的$r$是单增的,所以只需要添加操作)。然后暴力加上$[l,R]$的贡献,统计答案。再把$[l,R]$的贡献清掉,还原成$[R+1,pr]$的样子。
处理完一个块后,要把残余的信息清空。
取块大小为$\frac{n}{\sqrt{m}}$,复杂度还是$O(n\sqrt{m})$的,而且只需要考虑添加操作,在维护最大值的时候有奇效。
只考虑删除的同理。
二次离线莫队&在线莫队
不可能学的,这辈子都不可能学的。
板子+水题
糖果公园
树上+带修莫队板子。
long long ans[maxn],sum[maxn],all;
int be[maxn<<1],st[maxn],en[maxn],f[maxn<<1],tax[maxn],a[maxn],v[maxn],c[maxn],h[maxn],siz[maxn],son[maxn],top[maxn],deep[maxn],fa[maxn],num,cnt;
bool vis[maxn];
struct query{
int l,r,id,t,lc;
bool operator < (const query &x)const{
if(be[l]!=be[x.l])return l<x.l;
else if(be[r]!=be[x.r])return r<x.r;
return t<x.t;
}
}q[maxn];
struct modify{int x,y;}ch[maxn];
struct edge{int pre,to;}e[maxn<<1];
inline void add(int from,int to){e[++num]=(edge){h[from],to},h[from]=num;}
void dfs1(int node=1){
f[st[node]=++cnt]=node,siz[node]=1;
for(register int i=h[node],x;i;i=e[i].pre){
x=e[i].to;
if(siz[x])continue;
fa[x]=node,deep[x]=deep[node]+1;
dfs1(x),siz[node]+=siz[x];
if(siz[x]>siz[son[node]])son[node]=x;
}
f[en[node]=++cnt]=node;
}
void dfs2(int node=1){
siz[node]=0;
if(!son[node])return;
top[son[node]]=top[node],dfs2(son[node]);
for(register int i=h[node],x;i;i=e[i].pre){
x=e[i].to;
if(siz[x])top[x]=x,dfs2(x);
}
}
inline int lca(int x,int y){
while(top[x]!=top[y])deep[top[x]]<deep[top[y]]?y=fa[top[y]]:x=fa[top[x]];
return deep[x]<deep[y]?x:y;
}
inline void add(int x){all+=1ll*v[x]*c[++tax[x]];}
inline void del(int x){all-=1ll*v[x]*c[tax[x]--];}
inline void modify(int x){
if(vis[x])del(a[x]);
else add(a[x]);
vis[x]^=1;
}
int main(){
int n=read(),m=read(),t=read(),x,y,last=0,ql=0;
for(register int i=1;i<=m;++i)v[i]=read();
for(register int i=1;i<=n;++i)sum[i]=sum[i-1]+(c[i]=read());
for(register int i=1;i<n;++i)x=read(),y=read(),add(x,y),add(y,x);
dfs1(),dfs2();
for(register int i=1;i<=n;++i)a[i]=read();
for(register int i=1;i<=t;++i){
bool type=read();
if(!type)ch[++last].x=read(),ch[last].y=read();
else {
x=read(),y=read(),q[++ql].id=ql,q[ql].t=last;
int l=lca(x,y);
if(st[x]>st[y])swap(x,y);
if(l==x)q[ql].l=st[x],q[ql].r=st[y];
else q[ql].l=en[x],q[ql].r=st[y],q[ql].lc=l;
}
}
int sq=pow(cnt,2.0/3),len=cnt/sq+(bool)(cnt%sq),l=1,r=0,w=0;
for(register int i=1;i<=len;++i)
for(register int j=(i-1)*sq+1,r=min(j+sq-1,cnt);j<=r;++j)
be[j]=i;
sort(q+1,q+1+ql);
for(register int i=1;i<=ql;++i){
while(l<q[i].l)modify(f[l++]);
while(l>q[i].l)modify(f[--l]);
while(r>q[i].r)modify(f[r--]);
while(r<q[i].r)modify(f[++r]);
while(w<q[i].t){
x=ch[++w].x,y=ch[w].y;
if(vis[x])del(a[x]),add(y);
swap(a[x],ch[w].y);
}
while(w>q[i].t){
x=ch[w].x,y=ch[w].y;
if(vis[x])del(a[x]),add(y);
swap(a[x],ch[w--].y);
}
if(q[i].lc)add(a[q[i].lc]);
ans[q[i].id]=all;
if(q[i].lc)del(a[q[i].lc]);
}
for(register int i=1;i<=ql;++i)printf("%lld\n",ans[i]);
}
歴史の研究
回滚莫队板子。
long long ans[maxn],all;
int be[maxn],dis[maxn],a[maxn],tax[maxn];
struct query{
int l,r,id;
bool operator < (const query &x)const{
if(be[l]!=be[x.l])return l<x.l;
return r<x.r;
}
}q[maxn];
inline void add(int x){++tax[x],all=max(all,1ll*tax[x]*dis[x]);}
int main(){
int n=read(),m=read(),sq=n/sqrt(m),num=n/sq+(bool)(n%sq);
for(register int i=1;i<=num;++i)
for(register int j=(i-1)*sq+1,r=min(n,j+sq-1);j<=r;++j)
be[j]=i,dis[j]=a[j]=read();
sort(dis+1,dis+1+n);
int len=unique(dis+1,dis+1+n)-dis-1,b=0,r;
for(register int i=1;i<=n;++i)a[i]=lower_bound(dis+1,dis+1+len,a[i])-dis;
for(register int i=1;i<=m;++i)q[i].id=i,q[i].l=read(),q[i].r=read();
sort(q+1,q+1+m);
for(register int i=1;i<=m;++i){
if(be[q[i].l]!=b)b=be[q[i].l],all=0,memset(tax,0,sizeof tax),r=b*sq;
if(be[q[i].l]==be[q[i].r]){
for(register int j=q[i].l;j<=q[i].r;++j)add(a[j]);
ans[q[i].id]=all,all=0;
for(register int j=q[i].l;j<=q[i].r;++j)tax[a[j]]=0;
continue;
}
while(r<q[i].r)add(a[++r]);
long long rec=all;
for(register int j=b*sq;j>=q[i].l;--j)add(a[j]);
ans[q[i].id]=all,all=rec;
for(register int j=b*sq;j>=q[i].l;--j)--tax[a[j]];
}
for(register int i=1;i<=m;++i)printf("%lld\n",ans[i]);
}
【模板】回滚莫队
洛谷有回滚莫队板子辣!
维护两个桶$tl[i],tr[i]$,分别表示权值$i$出现的最靠左/右的位置。
左端点移动的时候记录被修改的桶原来的权值,没了。
ants
只加不删的回滚莫队。
暴力的做法是可撤销并查集,不过带个$\log$。
优美的做法是链表。对链表每一块元素维护左/右端点。如果新加的点两边有元素就合并起来,删除直接断开更新端点。这样就没有$\log$了。







